题目内容
已知R上的不间断函数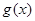 满足:①当
满足:①当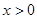 时,
时,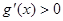 恒成立;②对任意的
恒成立;②对任意的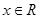 都有
都有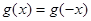 。又函数
。又函数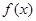 满足:对任意的
满足:对任意的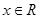 ,都有
,都有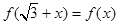 成立,当
成立,当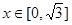 时,
时,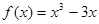 。若关于
。若关于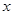 的不等式
的不等式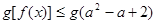 对
对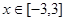 恒成立,则
恒成立,则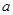 的取值范围( )
的取值范围( )
A.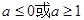 B.
B.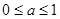 C.
C.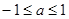 D.
D.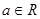
【答案】
A
【解析】
试题分析:当 时,
时,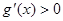 恒成立,所以当
恒成立,所以当 时
时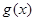 是增函数,对任意的
是增函数,对任意的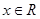 都有
都有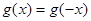 ,所以函数
,所以函数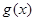 是偶函数,当
是偶函数,当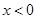 时是减函数,对任意的
时是减函数,对任意的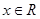 ,都有
,都有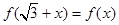 成立,所以函数
成立,所以函数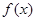 的周期
的周期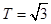 ,当
,当 时,
时,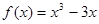
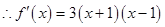 ,
,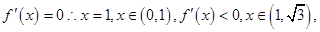
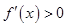
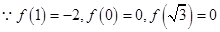
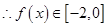
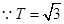
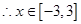 时
时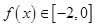 ,关于
,关于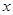 的不等式
的不等式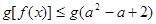 对
对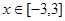 恒成立
恒成立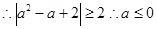 或
或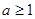
考点:函数性质的综合考察
点评:本题涉及到的函数性质有奇偶性,周期性,单调性等性质及利用导数求最值,数形结合法寻找关系式等思路,难度较大

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
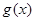 满足:①当
满足:①当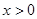 时,
时,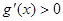 恒成立;②对任意的
恒成立;②对任意的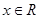 都有
都有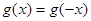 。又函数
。又函数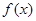 满足:对任意的
满足:对任意的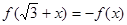 成立,当
成立,当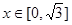 时,
时,
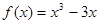 。若关于
。若关于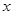 的不等式
的不等式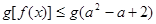 对
对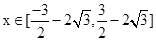 恒成立,则
恒成立,则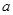 的取值范围( )
的取值范围( )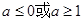 B.
B. 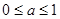 C.
C.
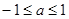 D.
D.