题目内容
已知R上的不间断函数![]() 满足:①当
满足:①当![]() 时,
时,![]() 恒成立;②对任意的
恒成立;②对任意的![]() 都有
都有![]() .又函数
.又函数![]() 满足:对任意的
满足:对任意的![]() ,都有
,都有![]() 成立,当
成立,当![]() 时,
时,![]() .若关于
.若关于![]() 的不等式
的不等式![]() 对
对![]() 恒成立,则
恒成立,则![]() 的取值范围_______________.
的取值范围_______________.
![]() 【解析】因为
【解析】因为![]() 满足当
满足当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 在(0,+∞)上单调递增, 又因为
在(0,+∞)上单调递增, 又因为![]() 满足对任意的
满足对任意的![]() 都有
都有![]() ,所以
,所以![]() 是偶函数. 因而不等式
是偶函数. 因而不等式![]() 等价于
等价于![]() .
.
对于函数f(x),当![]() 时,
时,![]() ,
,
![]() ,所以f(x)在x=1时有最小值-2.
,所以f(x)在x=1时有最小值-2.
![]() ,
,![]() ,f(x)max=
,f(x)max=![]() =2
=2
f(x)min=![]() =2.
=2.
![]() ,
,![]() .
.

练习册系列答案
相关题目
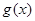 满足:①当
满足:①当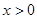 时,
时,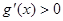 恒成立;②对任意的
恒成立;②对任意的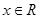 都有
都有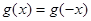 。又函数
。又函数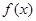 满足:对任意的
满足:对任意的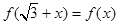 成立,当
成立,当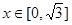 时,
时,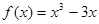 。若关于
。若关于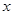 的不等式
的不等式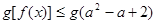 对
对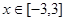 恒成立,则
恒成立,则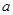 的取值范围( )
的取值范围( )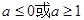 B.
B.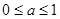 C.
C.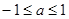 D.
D.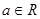
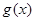 满足:①当
满足:①当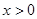 时,
时,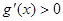 恒成立;②对任意的
恒成立;②对任意的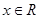 都有
都有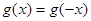 。又函数
。又函数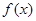 满足:对任意的
满足:对任意的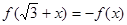 成立,当
成立,当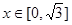 时,
时,
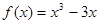 。若关于
。若关于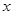 的不等式
的不等式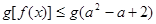 对
对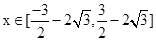 恒成立,则
恒成立,则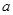 的取值范围( )
的取值范围( )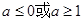 B.
B. 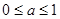 C.
C.
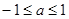 D.
D.