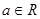题目内容
已知R上的不间断函数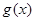 满足:①当
满足:①当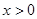 时,
时,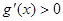 恒成立;②对任意的
恒成立;②对任意的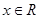 都有
都有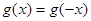 。又函数
。又函数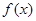 满足:对任意的
满足:对任意的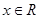 ,都有
,都有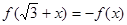 成立,当
成立,当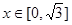 时,
时,
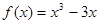 。若关于
。若关于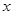 的不等式
的不等式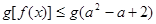 对
对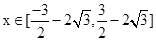 恒成立,则
恒成立,则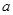 的取值范围( )
的取值范围( )
A.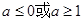 B.
B. 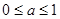 C.
C.
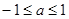 D.
D.
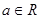
【答案】
A
【解析】解:因为函数g(x)满足:当x>0时,g'(x)>0恒成立且对任意x∈R都有g(x)=g(-x),则函数g(x)为R上的偶函数且在[0,+∞)上为单调递增函数,且有g|(x|)=g(x),
所以g[f(x)]≤g(a2-a+2)在R上恒成立⇔|f(x)|≤|a2-a+2|对x∈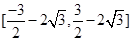 恒成立,只要使得定义域内|f(x)|max≤|a2-a+2|min,由于当
恒成立,只要使得定义域内|f(x)|max≤|a2-a+2|min,由于当 时,f(x)=x3-3x,
时,f(x)=x3-3x,
求导得:f′(x)=3x2-3=3(x+1)(x-1),该函数过点(-3,0),(0,0),(3,0),
且函数在x=-1处取得极大值f(-1)=2,在x=1处取得极小值f(1)=-2,又由于对任意的x∈R都有f(3+x)=-f(x)⇔f(2 +x)=-f(
+x)=-f( +x)=f(x)成立,则函数f(x)为周期函数且周期为T=
+x)=f(x)成立,则函数f(x)为周期函数且周期为T= ,所以函数f(x)在x∈
,所以函数f(x)在x∈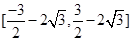 的最大值为2,所以令2≤|a2-a+2|解得:a≥1或a≤0.
的最大值为2,所以令2≤|a2-a+2|解得:a≥1或a≤0.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
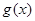 满足:①当
满足:①当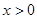 时,
时,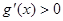 恒成立;②对任意的
恒成立;②对任意的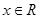 都有
都有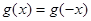 。又函数
。又函数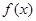 满足:对任意的
满足:对任意的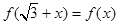 成立,当
成立,当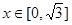 时,
时,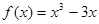 。若关于
。若关于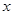 的不等式
的不等式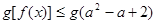 对
对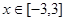 恒成立,则
恒成立,则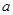 的取值范围( )
的取值范围( )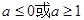 B.
B.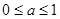 C.
C.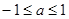 D.
D.