题目内容
已知二次函数f(x)=ax2+bx+c(a>0).
(Ⅰ)(i)若b=﹣2,且f(x)在(1,+∞)上为单调递增函数,求实数a的取值范围;
(ii)若b=﹣1,c=1,当x∈[0,1]时,|f(x)|的最大值为1,求实数a的取值范围;
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,求a的最小正整数值.
(Ⅰ)(i)[1,+∞);(ii)(0,1];(Ⅱ)5
解析试题分析:(Ⅰ)(i)若b=﹣2,则f(x)=ax2﹣2x+c(a>0)的图象是开口朝上且以直线x= 为对称轴的抛物线.若f(x)在(1,+∞)上为单调递增函数,则
为对称轴的抛物线.若f(x)在(1,+∞)上为单调递增函数,则 ≤1,解得a≥1,即实数a的取值范围为[1,+∞);(ii)若b=﹣1,c=1,则f(x)=ax2﹣x+1(a>0)的图象是开口朝上且以直线x=
≤1,解得a≥1,即实数a的取值范围为[1,+∞);(ii)若b=﹣1,c=1,则f(x)=ax2﹣x+1(a>0)的图象是开口朝上且以直线x=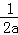 为对称轴的抛物线,若当x∈[0,1]时,|f(x)|的最大值为1,则
为对称轴的抛物线,若当x∈[0,1]时,|f(x)|的最大值为1,则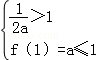 或
或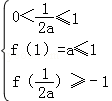 解得0<a<
解得0<a<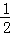 ,或
,或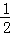 ≤a≤1,所以实数a的取值范围为(0,1];(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,则
≤a≤1,所以实数a的取值范围为(0,1];(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,则
解得a>4,故a的最小正整数值为5.
试题解析:(Ⅰ)(i)若b=﹣2,
则f(x)=ax2﹣2x+c(a>0)的图象是开口朝上且以直线x= 为对称轴的抛物线.
为对称轴的抛物线.
若f(x)在(1,+∞)上为单调递增函数,则 ≤1,解得a≥1,
≤1,解得a≥1,
即实数a的取值范围为[1,+∞)
(ii)若b=﹣1,c=1,
则f(x)=ax2﹣x+1(a>0)的图象是开口朝上且以直线x=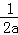 为对称轴的抛物线.
为对称轴的抛物线.
若当x∈[0,1]时,|f(x)|的最大值为1,
则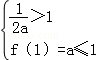 或
或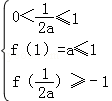 ,
,
解得0<a<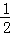 ,或
,或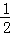 ≤a≤1
≤a≤1
综上所述:0<a≤1
即实数a的取值范围为(0,1]
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,
则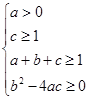
由b2>4ac>4a(1﹣a﹣b)得:
b2+4ab+4a2=(b+2a)2>4a,
即b+2a>2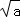 ,
,
即b>2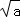 ﹣2a,…①
﹣2a,…①
由b2>4ac≥4a得:
b<﹣2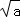 …②
…②
由①②得:
2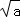 ﹣2a<﹣2
﹣2a<﹣2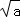 ,
,
解得a>4,
故a的最小正整数值为5.
考点:1.二次函数的图象与性质;2.不等式的性质

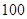
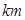 ,按交通法规定:这段公路车速限制在
,按交通法规定:这段公路车速限制在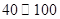 (单位:
(单位: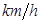 )之间.假设目前油价为
)之间.假设目前油价为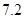 (单位:元
(单位:元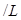 ),汽车的耗油率为
),汽车的耗油率为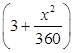 (单位:
(单位: ), 其中
), 其中 (单位:
(单位: 元,不考虑其它费用,这次租车的总费用最少是多少?此时的车速
元,不考虑其它费用,这次租车的总费用最少是多少?此时的车速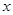 元,则本年度新增用电量
元,则本年度新增用电量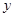 (亿千瓦时)与
(亿千瓦时)与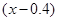 元成反比例.又当
元成反比例.又当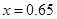 时,
时,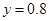 .
.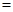 用电量
用电量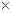 (实际电价-成本价)]
(实际电价-成本价)]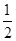 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用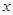 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数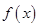 .
.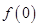 的值,并解释其实际意义;
的值,并解释其实际意义;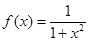 ,现有
,现有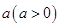 单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.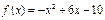 在区间[0,4]的最大值是
在区间[0,4]的最大值是 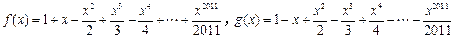 ,设
,设 内,则
内,则 的最小值为_________
的最小值为_________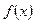 的图象经过点(9,
的图象经过点(9,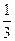 ), 则f(25)的值是_________.
), 则f(25)的值是_________. 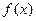 的图象过点
的图象过点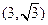 ,则
,则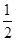 )时恒成立,求实数a的取值范围.
)时恒成立,求实数a的取值范围.