题目内容
一个口袋装有n个红球(n≥5且n∈N)和5个白球,一次摸奖从中摸2个球(每次摸奖后放回),2个球颜色不同则为中奖.
(1)试用n表示一次摸奖中奖的概率.
(2)若n=5,求3次摸奖的中奖次数ξ=1的概率及数学期望.
(3)记3次摸奖恰有1次中奖的概率为P,当n取多少时,P最大?
(1) P=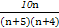 (2)
(2)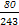
 (3) n=20
(3) n=20
解析

练习册系列答案
相关题目
某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
| 产品编号 | A1 | A2 | A3 | A4 | A5 |
| 质量指标(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| | | | | | |
| 产品编号 | A6 | A7 | A8 | A9 | A10 |
| 质量指标(x,y,z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(2)在该样本的一等品中,随机抽取2件产品,
①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.
某公司研制出一种新型药品,为测试该药品的有效性,公司选定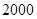 个药品样本分成三组,测试结果如下表:
个药品样本分成三组,测试结果如下表:
| 分组 | 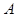 组 组 | 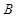 组 组 |  组 组 |
| 药品有效 | 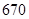 | 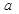 | 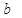 |
| 药品无效 | 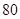 | 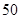 | 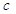 |
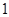 个,抽到
个,抽到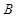 组药品有效的概率是
组药品有效的概率是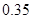 .
.(1)现用分层抽样的方法在全体样本中抽取
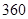 个测试结果,问应在
个测试结果,问应在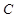 组抽取样本多少个? [来源:学优]
组抽取样本多少个? [来源:学优](2)已知
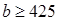 ,
,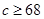 ,求该药品通过测试的概率(说明:若药品有效的概率不小于
,求该药品通过测试的概率(说明:若药品有效的概率不小于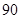 %,则认为测试通过).
%,则认为测试通过).  和
和 ,试求:
,试求:
 ,
, ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立. π(x∈R)是偶函数”为事件D,求事件D发生的概率.
π(x∈R)是偶函数”为事件D,求事件D发生的概率. ,乙在每局中获胜的概率为
,乙在每局中获胜的概率为 ,且各局胜负相互独立,比赛停止时一共已打
,且各局胜负相互独立,比赛停止时一共已打 局:
局: 年
年 月“神舟 ”发射成功.这次发射过程共有四个值得关注的环节,即发射、实验、授课、返回.据统计,由于时间关系,某班每位同学收看这四个环节的直播的概率分别为
月“神舟 ”发射成功.这次发射过程共有四个值得关注的环节,即发射、实验、授课、返回.据统计,由于时间关系,某班每位同学收看这四个环节的直播的概率分别为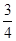 、
、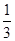 、
、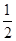 、
、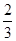 ,并且各个环节的直播收看互不影响.
,并且各个环节的直播收看互不影响. 名同学至少有
名同学至少有 名同学收看发射直播的概率;
名同学收看发射直播的概率;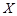 表示该班某一位同学收看的环节数,求
表示该班某一位同学收看的环节数,求 ,服用B有效的概率为
,服用B有效的概率为 .
.