题目内容
(本题满分12分)若函数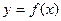 对任意
对任意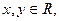 恒有
恒有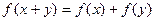 .
.
(1)指出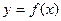 的奇偶性,并给予证明;
的奇偶性,并给予证明;
(2)若函数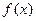 在其定义域上单调递减,对任意实数
在其定义域上单调递减,对任意实数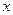 ,恒有
,恒有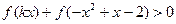 成立,求
成立,求 的取值范围.
的取值范围.
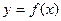 对任意
对任意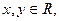 恒有
恒有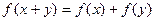 .
.(1)指出
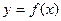 的奇偶性,并给予证明;
的奇偶性,并给予证明;(2)若函数
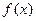 在其定义域上单调递减,对任意实数
在其定义域上单调递减,对任意实数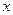 ,恒有
,恒有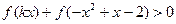 成立,求
成立,求 的取值范围.
的取值范围. 解:(1)令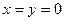 ,得
,得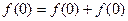 ,
, . ……1分
. ……1分
令 ,得
,得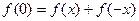 ,
,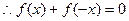 , ……3分
, ……3分
即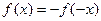 ,所以
,所以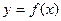 是奇函数. ……4分
是奇函数. ……4分
(2)∵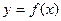 为R上单调递减
为R上单调递减 ∴由
∴由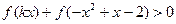 ,得
,得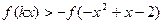 ,
,
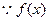 是奇函数,有
是奇函数,有 , ……8分
, ……8分
又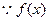 是R上的减函数,
是R上的减函数, , ……10分
, ……10分
即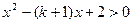 对于
对于 恒成立,
恒成立,
由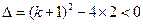 ,解得
,解得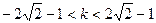 ……12分
……12分
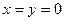 ,得
,得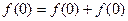 ,
, . ……1分
. ……1分令
 ,得
,得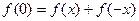 ,
,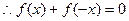 , ……3分
, ……3分即
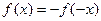 ,所以
,所以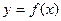 是奇函数. ……4分
是奇函数. ……4分(2)∵
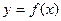 为R上单调递减
为R上单调递减 ∴由
∴由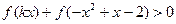 ,得
,得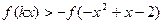 ,
,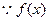 是奇函数,有
是奇函数,有 , ……8分
, ……8分又
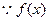 是R上的减函数,
是R上的减函数, , ……10分
, ……10分即
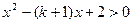 对于
对于 恒成立,
恒成立, 由
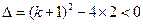 ,解得
,解得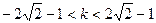 ……12分
……12分略

练习册系列答案
相关题目
 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且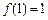 ,若任意的
,若任意的 ,当
,当 时,总有
时,总有 .
. ;
;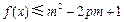 对所有的
对所有的 恒成立,其中
恒成立,其中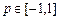 (
(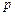 是常数),试用常数
是常数),试用常数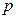 表示实数
表示实数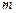 的取值范围.
的取值范围. ,
, ,解不等式
,解不等式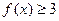 ; (2)如果
; (2)如果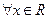 ,
,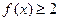 ,求a的取值范围
,求a的取值范围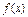 是定义在
是定义在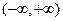 上的增函数,如果不等式
上的增函数,如果不等式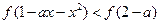 对于任意
对于任意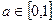 恒成立,求实数
恒成立,求实数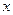 的取值范围;
的取值范围;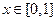 恒成立,求实数
恒成立,求实数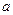 的取值范围.
的取值范围.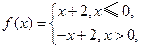 则不等式
则不等式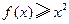 的解集为( )
的解集为( ) 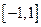
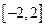
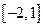
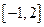
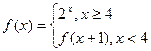 ,则
,则 ,
,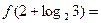 .
.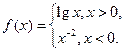 若
若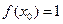 ,则
,则 的值是 .
的值是 .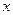 ,符号[
,符号[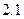 ]=2;[
]=2;[ ]=
]= , 这个函数[
, 这个函数[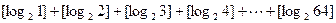 的值为
的值为