题目内容
已知曲线C的极坐标方程为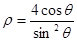 ,直线
,直线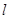 的参数方程为
的参数方程为 ( t为参数,0≤
( t为参数,0≤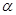 <
<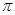 ).
).
(Ⅰ)把曲线C的极坐标方程化为直角坐标方程,并说明曲线C的形状;
(Ⅱ)若直线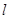 经过点(1,0),求直线
经过点(1,0),求直线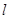 被曲线C截得的线段AB的长.
被曲线C截得的线段AB的长.
【答案】
(Ⅰ) 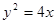 ,抛物线;(Ⅱ)8
,抛物线;(Ⅱ)8
【解析】
试题分析:(1)将已知极坐标方程变形为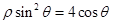 ,再两边同时乘以
,再两边同时乘以 ,利用
,利用
 化为直角坐标方程,并判断曲线形状;(2)由直线
化为直角坐标方程,并判断曲线形状;(2)由直线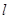 经过点(1,0)和(0,1),确定倾斜角
经过点(1,0)和(0,1),确定倾斜角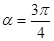 ,从而确定参数方程,再将直线的参数方程代入曲线C的直角坐标方程,得关于
,从而确定参数方程,再将直线的参数方程代入曲线C的直角坐标方程,得关于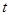 的一元二次方程,结合
的一元二次方程,结合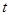 的几何意义,线段AB的长
的几何意义,线段AB的长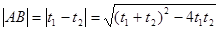 ,利用韦达定理求解.
,利用韦达定理求解.
试题解析:(1)曲线C的直角坐标方程为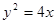 ,故曲线C是顶点为O(0,0),焦点为F(1,0)的抛物线;
,故曲线C是顶点为O(0,0),焦点为F(1,0)的抛物线;
(2)直线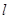 的参数方程为
的参数方程为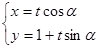 ( t为参数,0≤
( t为参数,0≤ <
< ).故l经过点(0,1);若直线
).故l经过点(0,1);若直线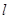 经过点(1,0),则
经过点(1,0),则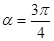
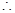 直线
直线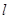 的参数方程为
的参数方程为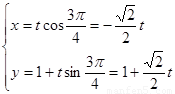 (t为参数)
(t为参数)
代入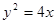 ,得
,得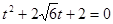
设A、B对应的参数分别为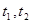 ,则
,则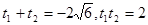
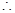
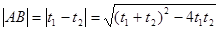 =8
=8
考点:1、极坐标方程和直角坐标方程的转换;2、直线的参数方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
