题目内容
平面直角坐标系中,直线l的参数方程是
(t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为ρ2cos2θ+ρ2sin2θ-2ρsinθ-3=0.
(1)求直线l的极坐标方程;
(2)若直线l与曲线C相交于A、B两点,求|AB|.
|
(1)求直线l的极坐标方程;
(2)若直线l与曲线C相交于A、B两点,求|AB|.
分析:(1)将直线化成普通方程,可得它是经过原点且倾斜角为
的直线,由此不难得到直线l的极坐标方程;
(2)将直线l的极坐标方程代入曲线C极坐标方程,可得关于ρ的一元二次方程,然后可以用根与系数的关系结合配方法,可以得到AB的长度.
| π |
| 3 |
(2)将直线l的极坐标方程代入曲线C极坐标方程,可得关于ρ的一元二次方程,然后可以用根与系数的关系结合配方法,可以得到AB的长度.
解答:解:(1)直线l的参数方程是
(t为参数),化为普通方程得:y=
x
∴在平面直角坐标系中,直线l经过坐标原点,倾斜角是
,
因此,直线l的极坐标方程是θ=
,(ρ∈R); …(5分)
(2)把θ=
代入曲线C的极坐标方程ρ2cos2θ+ρ2sin2θ-2ρsinθ-3=0,得ρ2-
ρ-3=0
∴由一元二次方程根与系数的关系,得ρ1+ρ2=
,ρ1ρ2=-3,
∴|AB|=|ρ1-ρ2|=
=
. …(10分)
|
| 3 |
∴在平面直角坐标系中,直线l经过坐标原点,倾斜角是
| π |
| 3 |
因此,直线l的极坐标方程是θ=
| π |
| 3 |
(2)把θ=
| π |
| 3 |
| 3 |
∴由一元二次方程根与系数的关系,得ρ1+ρ2=
| 3 |
∴|AB|=|ρ1-ρ2|=
| (ρ1+ρ2)2-4ρ1ρ2 |
| 15 |
点评:本题以参数方程和极坐标方程为例,考查了两种方程的互化和直线与圆锥曲线的位置关系等知识点,属于基础题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 如图,平面直角坐标系中,A(
如图,平面直角坐标系中,A(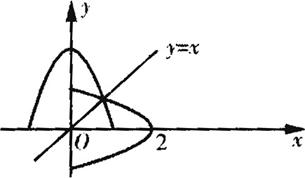
 ,2),B(-
,2),B(- ,-
,-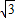 ),将其所在纸面沿x轴折成直二面角,则折起后的A,B两点的距离是 .
),将其所在纸面沿x轴折成直二面角,则折起后的A,B两点的距离是 .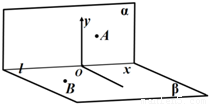
 ,2),B(-
,2),B(- ,-
,- ),将其所在纸面沿x轴折成直二面角,则折起后的A,B两点的距离是 .
),将其所在纸面沿x轴折成直二面角,则折起后的A,B两点的距离是 .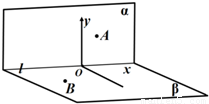
 ,2),B(-
,2),B(- ,-
,-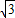 ),将其所在纸面沿x轴折成直二面角,则折起后的A,B两点的距离是 .
),将其所在纸面沿x轴折成直二面角,则折起后的A,B两点的距离是 .