题目内容
(本小题共14分)
设函数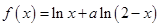 .
.
(Ⅰ)求函数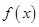 的定义域及其导数
的定义域及其导数 ;
;
(Ⅱ)当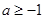 时,求函数
时,求函数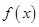 的单调区间;
的单调区间;
(Ⅲ)当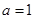 时,令
时,令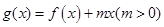 ,若
,若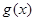 在
在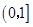 上的最大值为
上的最大值为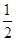 ,求实数
,求实数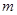 的值.
的值.
【答案】
(1)(0,2),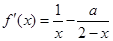
(2)函数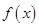 的单调递增区间是
的单调递增区间是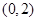
(3)
【解析】解:(Ⅰ)由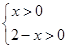 得
得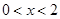 ,即函数的定义域为(0,2); -----------------2分
,即函数的定义域为(0,2); -----------------2分
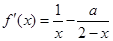 .
---------------------4分
.
---------------------4分
(Ⅱ)当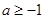 时,
时, 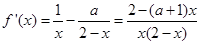
(1)当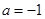 时,
时,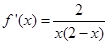 ,所以在区间
,所以在区间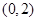 上,
上,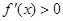 ,
,
故函数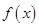 的单调递增区间是
的单调递增区间是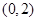 ;
---------------------5分
;
---------------------5分
(2)当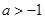 时,令
时,令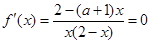 ,解得
,解得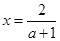 ,
,
①当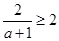 时,即
时,即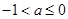 时,在区间
时,在区间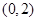 上,
上,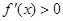 ,
,
故函数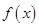 的单调递增区间是
的单调递增区间是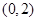 ;
---------------------7分
;
---------------------7分
②当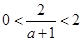 时,即
时,即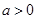 时,在区间
时,在区间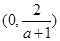 上,
上,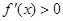 ,
,
在区间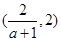 上,
上,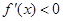 ,故函数
,故函数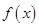 的单调递增区间是
的单调递增区间是
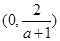 ,单调递减区间是
,单调递减区间是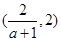 .
---------------------9分
.
---------------------9分
(Ⅲ) 当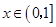 且
且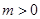 时,
时, ,
,
--------------------11分
即函数在区间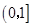 上是增函数,故函数
上是增函数,故函数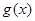 在
在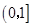 上的最大值为
上的最大值为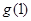 ,
,
--------------------12分
所以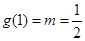 ,即
,即 .
--------------------14分
.
--------------------14分

练习册系列答案
相关题目

 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF
 的棱长为
的棱长为 ,
, 是
是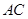 与
与 的交点,
的交点, 为
为 的中点.
的中点. ∥平面
∥平面 ;
; 平面
平面 ;
; 的体积.
的体积.