题目内容
(选做题)已知点P(1+cosα,sinα),参数α∈[0,π],点Q在曲线C:ρ=
上.
(I)求点P的轨迹方程和曲线C的直角坐标方程;
(II)求|PQ|的最小值.
| 10 | ||||
-
|
(I)求点P的轨迹方程和曲线C的直角坐标方程;
(II)求|PQ|的最小值.
分析:(I)由
消去α得点P的轨迹方程,利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得C的直角坐标方程
(II)根据直线和圆的位置关系求解|PQ|的最小值
|
(II)根据直线和圆的位置关系求解|PQ|的最小值
解答:解:(I)由
消去α得点P的轨迹方程为(x-1)2+y2=1,(y≥0).
C:ρ=
即为-
ρsin(θ+
)=10,-(ρsinθ+ρcosθ)=10
直角坐标方程为x+y=-10.
(II)点P的轨迹是以(1,0)为圆心,以1为半径的上半圆,当Q为坐标原点时,
|PQ|的最小值=5
|
C:ρ=
| 10 | ||||
-
|
| 2 |
| π |
| 4 |
直角坐标方程为x+y=-10.
(II)点P的轨迹是以(1,0)为圆心,以1为半径的上半圆,当Q为坐标原点时,
|PQ|的最小值=5
| 2 |
点评:本题考查了极坐标和直角坐标的互化及参数方程与普通方程的互化,能在直角坐标系中利用数形结合的思想求出最值,属于基础题.本题要注意P的轨迹是半圆.

练习册系列答案
相关题目
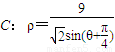 上.
上.