题目内容
(2008•深圳一模)(不等式选讲选做题)已知点P是边长为2
的等边三角形内一点,它到三边的距离分别为x、y、z,则x、y、z所满足的关系式为
| 3 |
x+y+z=3
x+y+z=3
,x2+y2+z2的最小值是3
3
.分析:设等边三角形的边长为a,高为h将P与三角形的各顶点连接,进而分别表示出三角形三部分的面积,相加应等于总的面积建立等式求得x+y+z的值;再利用:(x2+y2+z2)×(1+1+1 )≥(x+y+z)2这个不等关系进行求最小值即可.
解答:解:设等边三角形的边长为a,高为h
将P与三角形的各顶点连接
根据面积
那么:
ax+
ay+
az=
ah
所以x+y+z=h
因为等边三角形的边长为2
,所以高为h=3
所以x.y.z所满足的关系是为:x+y+z=3
∵(x2+y2+z2)×(1+1+1 )≥(x+y+z)2=9,
∴x2+y2+z2≥9×
=3,
故 x2+y2+z2的最小值为3,
故答案为:x+y+z=3;3.
将P与三角形的各顶点连接
根据面积
那么:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以x+y+z=h
因为等边三角形的边长为2
| 3 |
所以x.y.z所满足的关系是为:x+y+z=3
∵(x2+y2+z2)×(1+1+1 )≥(x+y+z)2=9,
∴x2+y2+z2≥9×
| 1 |
| 3 |
故 x2+y2+z2的最小值为3,
故答案为:x+y+z=3;3.
点评:本题主要考查了三角形中的几何计算、平均值不等式在函数极值中的应用,考查了学生综合分析问题的能力和转化和化归的思想.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
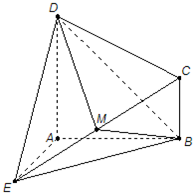 (2008•深圳一模)如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥AB,M是EC的中点.
(2008•深圳一模)如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥AB,M是EC的中点.