题目内容
(2012•太原模拟)(选做题)已知点P(1+cosα,sinα),参数a∈[0,π],点Q在曲线C:ρ=
上.
(1)求点P的轨迹方程和曲线C的直角坐标方程;
(2)求点P与点Q之间距离的最小值.
| 9 | ||||
|
(1)求点P的轨迹方程和曲线C的直角坐标方程;
(2)求点P与点Q之间距离的最小值.
分析:(1)先将
和由C:ρ=
消去参数或利用极坐标与直角坐标的关系化得点P的轨迹方程和曲线C的直角坐标方程即可;
(2)先求出半圆(x-1)2+y2=1(y≥0)的圆心(1,0)到直线x+y=9的距离d,从而利用点P与点Q之间距离的最小值为d-r即得.
|
| 9 | ||||
|
(2)先求出半圆(x-1)2+y2=1(y≥0)的圆心(1,0)到直线x+y=9的距离d,从而利用点P与点Q之间距离的最小值为d-r即得.
解答:解:(1)由
得点P的轨迹方程(x-1)2+y2=1(y≥0),
又由C:ρ=
得ρ=
,∴ρsinθ+ρcosθ=9,
∴曲线C的直角坐标方程x+y=9.
(2)半圆(x-1)2+y2=1(y≥0)的圆心(1,0)到直线x+y=9的距离为d=
=4
,
∴点P与点Q之间距离的最小值=4
-1.
|
又由C:ρ=
| 9 | ||||
|
| 9 |
| sinθ+cosθ |
∴曲线C的直角坐标方程x+y=9.
(2)半圆(x-1)2+y2=1(y≥0)的圆心(1,0)到直线x+y=9的距离为d=
| |1-9| | ||
|
| 2 |
∴点P与点Q之间距离的最小值=4
| 2 |
点评:本小题主要考查参数方程化成普通方程、点到直线的距离公式、简单曲线的极坐标方程等基础知识,考查运算求解能力,考查转化思想.属于基础题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
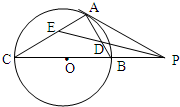 (2012•太原模拟)选修4-1:几何证明选讲
(2012•太原模拟)选修4-1:几何证明选讲