题目内容
【题目】在平面直角坐标系xOy中,椭圆E:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,焦距为2.
,焦距为2.

(1)求椭圆E的方程;
(2)如图,动直线l:y=k1x-![]() 交椭圆E于A,B两点,C是椭圆E上一点,直线OC的斜率为k2,且k1k2=
交椭圆E于A,B两点,C是椭圆E上一点,直线OC的斜率为k2,且k1k2=![]() .M是线段OC延长线上一点,且|MC|∶|AB|=2∶3,⊙M的半径为|MC|,OS,OT是⊙M的两条切线,切点分别为S,T.求∠SOT的最大值,并求取得最大值时直线l的斜率.
.M是线段OC延长线上一点,且|MC|∶|AB|=2∶3,⊙M的半径为|MC|,OS,OT是⊙M的两条切线,切点分别为S,T.求∠SOT的最大值,并求取得最大值时直线l的斜率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题分析:由椭圆焦距为![]() 可得
可得![]() ,由离心率为
,由离心率为![]() 可得
可得![]() ,根据
,根据![]() 可得
可得![]() ,从而可得椭圆的标准方程;(2)直线方程与所求椭圆方程联立消去
,从而可得椭圆的标准方程;(2)直线方程与所求椭圆方程联立消去![]() ,可得
,可得![]() ,根据韦达定理与弦长公式可得可求出
,根据韦达定理与弦长公式可得可求出![]() 的长,从而求出圆的半径,可得到
的长,从而求出圆的半径,可得到![]() 斜率,设出直线
斜率,设出直线![]() 的方程,与椭圆方程联立,求出
的方程,与椭圆方程联立,求出![]() 点坐标,可得
点坐标,可得![]() 的长,可求得
的长,可求得![]() ,求出
,求出![]() 的取值范围,从而可得
的取值范围,从而可得![]() 的最大值,进而可得结果.
的最大值,进而可得结果.
试题解析:(1)由题意知e=![]() =
=![]() ,2c=2,所以a=
,2c=2,所以a=![]() ,b=1,
,b=1,
所以椭圆E的方程为![]() +y2=1.
+y2=1.
(2)设A(x1,y1),B(x2,y2),
联立方程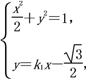 得(4k+2)x2-4
得(4k+2)x2-4![]() k1x-1=0.
k1x-1=0.
由题意知Δ>0,且x1+x2=![]() ,x1x2=-
,x1x2=-![]() ,
,
所以|AB|=![]() |x1-x2|
|x1-x2|
=![]()
![]() .
.
由题意可知圆M的半径r为
r=![]() |AB|=
|AB|=![]()
![]() .
.
由题设知k1k2=![]() ,所以k2=
,所以k2=![]() ,
,
因此直线OC的方程为y=![]() x.
x.
联立方程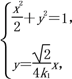
得x2=![]() ,y2=
,y2=![]() ,
,
因此|OC|=![]() =
=![]() .
.
由题意可知sin![]() =
=![]() =
=![]() ,
,
而![]() =
=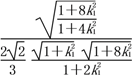
=![]()
![]() ,
,
令t=1+2k,则t>1,![]() ∈(0,1),
∈(0,1),
因此![]() =
=![]()
![]() =
=![]()

=![]()
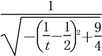 ≥1,
≥1,
当且仅当![]() =
=![]() ,即t=2时等号成立,此时k1=±
,即t=2时等号成立,此时k1=±![]() ,
,
所以sin![]() ≤
≤![]() ,因此
,因此![]() ≤
≤![]() ,
,
所以∠SOT的最大值为![]() .
.
综上所述:∠SOT的最大值为![]() ,取得最大值时直线l的斜率为k1=±
,取得最大值时直线l的斜率为k1=±![]() .
.

【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: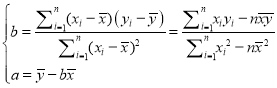
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了了解人们]对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15∽65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
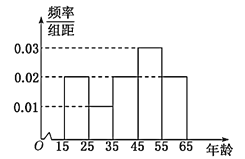
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率.
②记抽到45岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]()
