题目内容
已知函数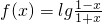 .
.
(1)求f(x)的定义域;
(2)求该函数的反函数f-1(x);
(3)判断f-1(x)的奇偶性.
解:(1)由  >0 解得-1<x<1,故函数的定义域是(-1,1).
>0 解得-1<x<1,故函数的定义域是(-1,1).
(2)由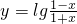 ,得
,得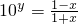 (y∈R),所以,
(y∈R),所以,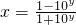 ,
,
所求反函数为 f-1(x)=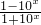 (x∈R).
(x∈R).
(3)f-1(-x)=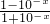 =
=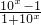 =-f-1(x),所以,f-1(x)是奇函数.
=-f-1(x),所以,f-1(x)是奇函数.
分析:(1)由 >0 解得-1<x<1,即得函数的定义域.
>0 解得-1<x<1,即得函数的定义域.
(2)由函数的解析式求出自变量,再把自变量和函数交换位置,即得反函数的解析式,注明反函数的定义域.
(3)由f-1(-x)=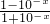 =
=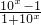 =-f-1(x),可得 f-1(x)是奇函数.
=-f-1(x),可得 f-1(x)是奇函数.
点评:本题考查求函数的定义域,求反函数,以及函数的奇偶性的判断方法,求出反函数,是解题的难点.
 >0 解得-1<x<1,故函数的定义域是(-1,1).
>0 解得-1<x<1,故函数的定义域是(-1,1).(2)由
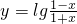 ,得
,得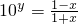 (y∈R),所以,
(y∈R),所以,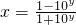 ,
,所求反函数为 f-1(x)=
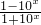 (x∈R).
(x∈R).(3)f-1(-x)=
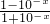 =
=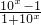 =-f-1(x),所以,f-1(x)是奇函数.
=-f-1(x),所以,f-1(x)是奇函数.分析:(1)由
 >0 解得-1<x<1,即得函数的定义域.
>0 解得-1<x<1,即得函数的定义域.(2)由函数的解析式求出自变量,再把自变量和函数交换位置,即得反函数的解析式,注明反函数的定义域.
(3)由f-1(-x)=
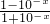 =
=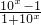 =-f-1(x),可得 f-1(x)是奇函数.
=-f-1(x),可得 f-1(x)是奇函数.点评:本题考查求函数的定义域,求反函数,以及函数的奇偶性的判断方法,求出反函数,是解题的难点.

练习册系列答案
相关题目
 .
. .
. 的图象在x轴上方?
的图象在x轴上方? .
. 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值.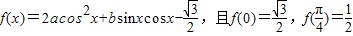 .
. .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.