题目内容
样本(x1，x2，…，xn)的平均数为x，样本(y1，y2，…，ym)的平均数为y(x≠y)．若样本(x1，x2，…，xn，y1，y2，…，ym)的平均数z＝αx＋(1－α)y，其中0<α<
，则n，m的大小关系为( )
，则n，m的大小关系为( )| A．n<m | B．n>m | C．n＝m | D．不能确定 |
A
由题意知，样本(x1，…，xn，y1，…，ym)的平均数为z＝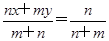
x＋
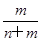y，且z＝αx＋(1－α)y，所以α＝
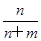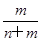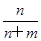，1－α＝.又因为0<α<，所以0<<，解得n<m.故选A.
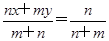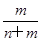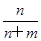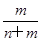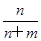x＋y，且z＝αx＋(1－α)y，所以α＝，1－α＝.又因为0<α<，所以0<<，解得n<m.故选A.
练习册系列答案
快乐5加2金卷系列答案
相关题目
,则( )
、
、
、
、
.若用分层抽样的方法从样本中抽取分数在
范围内的数据
个，则其中分数在
个
个
个
个
的样本的重量的频率分布直方图，样本重量均在
内，其分组为
，
，
，则样本重量落在
