题目内容
设函数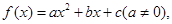 曲线y=f(x)通过点(0,2a+3),且在点
曲线y=f(x)通过点(0,2a+3),且在点
(-1,f(-1))处的切线垂直于y轴.
(1)用a分别表示b和c;
(2)当bc取得最小值时,求函数g(x)=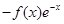 的单调区间.
的单调区间.
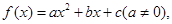 曲线y=f(x)通过点(0,2a+3),且在点
曲线y=f(x)通过点(0,2a+3),且在点(-1,f(-1))处的切线垂直于y轴.
(1)用a分别表示b和c;
(2)当bc取得最小值时,求函数g(x)=
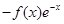 的单调区间.
的单调区间.(1)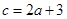 b=2a
b=2a
(2)见解析
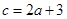 b=2a
b=2a(2)见解析
(1)因为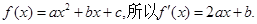
又因为曲线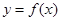 通过点(0,2a+3),
通过点(0,2a+3),
故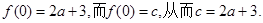
又曲线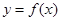 在(-1,f(-1))处的切线垂直于y轴,故
在(-1,f(-1))处的切线垂直于y轴,故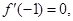
即-2a+b=0,因此b=2a.
(2)由(1)得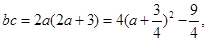
故当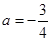 时,
时,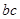 取得最小值-
取得最小值-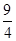 .
.
此时有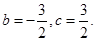
从而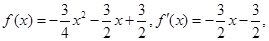
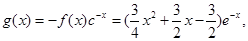
所以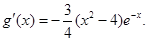
令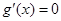 ,解得
,解得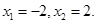
当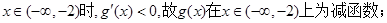
当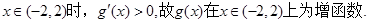
当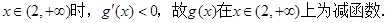
由此可见,函数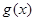 的单调递减区间为(-∞,-2)、(2,+∞);单调递增区间为(-2,2).
的单调递减区间为(-∞,-2)、(2,+∞);单调递增区间为(-2,2).
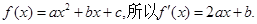
又因为曲线
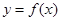 通过点(0,2a+3),
通过点(0,2a+3),故
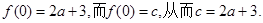
又曲线
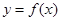 在(-1,f(-1))处的切线垂直于y轴,故
在(-1,f(-1))处的切线垂直于y轴,故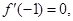
即-2a+b=0,因此b=2a.
(2)由(1)得
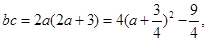
故当
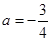 时,
时,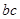 取得最小值-
取得最小值-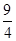 .
.此时有
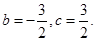
从而
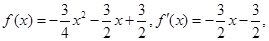
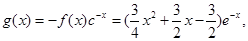
所以
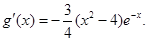
令
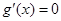 ,解得
,解得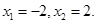
当
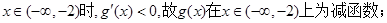
当
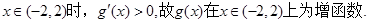
当
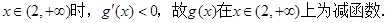
由此可见,函数
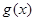 的单调递减区间为(-∞,-2)、(2,+∞);单调递增区间为(-2,2).
的单调递减区间为(-∞,-2)、(2,+∞);单调递增区间为(-2,2).
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, .
. 的极值;(2)若
的极值;(2)若 恒成立,求实数
恒成立,求实数 的值;
的值;
 有两个极值点
有两个极值点 、
、 (
(
 的取值范围,并证明
的取值范围,并证明 .
. ,函数
,函数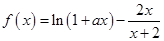 .
.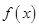 在区间
在区间 上的单调性;
上的单调性;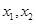 ,且
,且 ,求
,求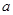 的取值范围.
的取值范围. 是二次函数,方程
是二次函数,方程 有两个相等的实数根,且
有两个相等的实数根,且 。
。 把
把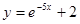 在点
在点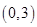 处的切线方程为 .
处的切线方程为 . ;
; .
. 在
在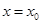 处取最大值。以下各式正确的序号为 .
处取最大值。以下各式正确的序号为 .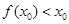 ②
②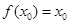 ③
③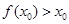 ④
④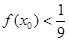 ⑤
⑤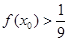
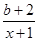 (x>1),其中b为实数.
(x>1),其中b为实数.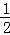 对称,且f′(1)=0
对称,且f′(1)=0