题目内容
适当增加不等式条件使下列命题成立:
(1)若a>b,则ac≤bc;
(2)若ac2>bc2,则a2>b2;
(3)若a>b,则lg(a+1)>lg(b+1);
(4)若a>b,c>d,则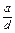 >
>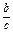 ;
;
(5)若a>b,则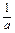 <
<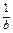 .
.
(1)若a>b,则ac≤bc;
(2)若ac2>bc2,则a2>b2;
(3)若a>b,则lg(a+1)>lg(b+1);
(4)若a>b,c>d,则
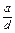 >
>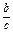 ;
;(5)若a>b,则
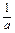 <
<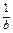 .
.1)增加条件“c≤0”.(2)增加条件“b≥0”.(3)应加条件“b>-1”.(4)增加条件为“a<0,c>0,d<0”.(5) 增加条件为“ab>0”.
(1)原命题改为:若a>b且c≤0,则ac≤bc,即增加条件“c≤0”.
(2)由ac2>bc2可得a>b,但只有b≥0时,才有a2>b2,即增加条件“b≥0”.
(3)由a>b可得a+1>b+1,但作为真数,应有b+1>0,故应加条件“b>-1”.
(4)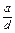 >
>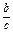 成立的条件有多种,如a>b>0,c>d>0,因此可增加条件“b>0,d>0”.还可增加条件为“a<0,c>0,d<0”.
成立的条件有多种,如a>b>0,c>d>0,因此可增加条件“b>0,d>0”.还可增加条件为“a<0,c>0,d<0”.
(5)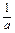 <
<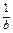 成立的条件是a>b,ab>0或a<0,b>0,
成立的条件是a>b,ab>0或a<0,b>0,
故增加条件为“ab>0”.
(2)由ac2>bc2可得a>b,但只有b≥0时,才有a2>b2,即增加条件“b≥0”.
(3)由a>b可得a+1>b+1,但作为真数,应有b+1>0,故应加条件“b>-1”.
(4)
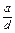 >
>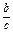 成立的条件有多种,如a>b>0,c>d>0,因此可增加条件“b>0,d>0”.还可增加条件为“a<0,c>0,d<0”.
成立的条件有多种,如a>b>0,c>d>0,因此可增加条件“b>0,d>0”.还可增加条件为“a<0,c>0,d<0”.(5)
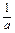 <
<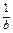 成立的条件是a>b,ab>0或a<0,b>0,
成立的条件是a>b,ab>0或a<0,b>0,故增加条件为“ab>0”.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
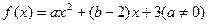 ,若不等式
,若不等式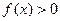 的解集为
的解集为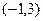 。
。 (1)求
(1)求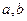 的值;
的值;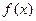 在
在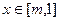 上的最小值为1,求实数
上的最小值为1,求实数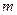 的值。
的值。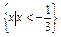 ,求关于x的不等式(a-3b)x+(b-2a)>0的解集.
,求关于x的不等式(a-3b)x+(b-2a)>0的解集.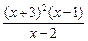 ≤0的解集是
≤0的解集是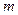 是什么实数时,关于
是什么实数时,关于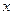 的一元二次方程
的一元二次方程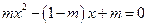 没有实数根?
没有实数根?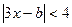 的解集中的整数有且仅有1,2,3,则
的解集中的整数有且仅有1,2,3,则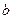 的取值范围是
的取值范围是 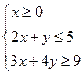 ,那么
,那么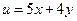 的最小值为
的最小值为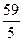
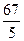
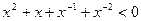 的解集是_____________。
的解集是_____________。