题目内容
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,依次连接椭圆的四个顶点得到的菱形面积为4.
,依次连接椭圆的四个顶点得到的菱形面积为4.
(1)求椭圆的方程;
(2)过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,设
两点,设![]() 与
与![]() 面积之比为
面积之比为![]() (其中
(其中![]() 为坐标原点),当
为坐标原点),当![]() 时,求实数
时,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]() 或
或![]()
【解析】试题分析: ![]() 根据题意离心率为
根据题意离心率为![]() ,依次连接椭圆的四个顶点得到的菱形面积为4,列出方程求出椭圆方程(2) 设直线
,依次连接椭圆的四个顶点得到的菱形面积为4,列出方程求出椭圆方程(2) 设直线![]() 方程为
方程为![]() ,联立直线与椭圆方程,求出
,联立直线与椭圆方程,求出
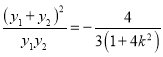 ,由题意
,由题意![]() ,求出
,求出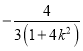 的取值范围,求出
的取值范围,求出![]() 的表达式,代入求出范围
的表达式,代入求出范围
解析:(1)∵椭圆![]() 的离心率为
的离心率为![]() ,且依次连接椭圆的四个顶点得到的菱形面积为4,
,且依次连接椭圆的四个顶点得到的菱形面积为4,
∴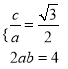 ,∴
,∴![]() ,即椭圆方程为
,即椭圆方程为![]() .
.
(2)由题意得设直线![]() 方程为
方程为![]() ,其中
,其中![]() ,代入椭圆方程得:
,代入椭圆方程得: ![]() ,
,
则有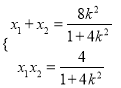 ,从而有
,从而有![]()
![]() ,①
,①
![]()
![]()
![]() ,②
,②
由①②可得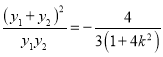 ,
,
由![]() 得
得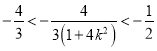 .又
.又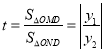 ,因
,因![]() ,
,
故![]() ,又
,又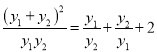
![]() ,
,
从而有![]() ,得
,得![]() ,解得
,解得![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目