题目内容
设正四面体的四个顶点是 各棱长均为1米,有一个小虫从点
各棱长均为1米,有一个小虫从点 开始按以下规则前进:在每一顶点处用同样的概率选择通过这个顶点的三条棱之一,并一直爬到这条 棱的尽头,则它爬了
开始按以下规则前进:在每一顶点处用同样的概率选择通过这个顶点的三条棱之一,并一直爬到这条 棱的尽头,则它爬了 米之后恰好再次位于顶点
米之后恰好再次位于顶点 的概率是 (结果用分数表示).
的概率是 (结果用分数表示).
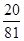
解析试题分析:小虫从A出发,一共分第5步走,可以确定下来是小虫最后一步必须回到A,那么第四步就不能是走回A,所以第三步成为关键,
分两种情况,①回到A点,②不回A点。
在①情况下,小虫第一步有3种选择,第三步为了回到A,则第二步只能有2种选择,到第四步时,因为从A出发,又有3种选择,所以此时共3×2×1×3×1=18种可能。
在②情况下,第二步的走法又分为③回A点或者④不回A点的情况。
因此在③情况下,共3×1×3×2×1=18种可能,
在④情况下,共3×2×2×2×1=24种可能。
所以,第五步回到A总共有18+18+24=60种可能。
而小虫总共有3×3×3×3×3=243种选择,
故它爬了 米之后恰好再次位于顶点
米之后恰好再次位于顶点 的概率是
的概率是 。
。
考点:本题主要考查等可能性事件的概率计算。
点评:中档题,利用分类分步计数原理,计算完成事件的方法数,是正确解题的关键。

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 -
- )6的二项展开式中的常数项为_____.(用数字作答)
)6的二项展开式中的常数项为_____.(用数字作答) 的展开式中,含
的展开式中,含 的项的系数是 .
的项的系数是 . 的展开式中,
的展开式中, 项的系数是 (用数字作答).
项的系数是 (用数字作答). (n为正偶数)的展开式中第5项的二项式系数最大,则第5项是 .
(n为正偶数)的展开式中第5项的二项式系数最大,则第5项是 . 的展开式中,系数最大的项是第 项
的展开式中,系数最大的项是第 项