题目内容
【题目】某校为了解全校高中学生五一小长假参加实践活动的情况,抽查了100名学生,统计他们假期参加实践活动的时间,绘成的频率分布直方图如图所示.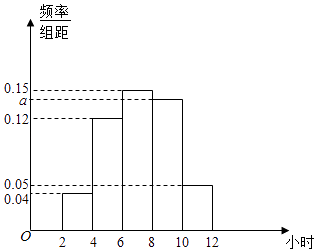
(1)求这100名学生中参加实践活动时间在6~10小时内的人数;
(2)估计这100名学生参加实践活动时间的众数、中位数和平均数.
【答案】
(1)【解答】解:依题意,100名学生中参加实践活动的时间在6~10小时内的人数为:
100×[1﹣(0.04+0.12+0.05)×2]=58,
即这100名学生中参加实践活动时间在6~10小时内的人数为58.
(2)【解答】解:由频率分布直方图可以看出最高矩形横轴上的中点为7,
故这100名学生参加实践活动时间的众数的估计值为7小时,
由(0.04+0.12+0.15+a+0.05)×2=1,解得a=0.14,
则6+ ![]() ,
,
即这100名学生参加实践活动时间的中位数为7.2小时,
这100名学生参加实践活动时间的平均数为:
0.04×2×3+0.12×2×5+0.15×2×7+0.14×2×9+0.05×2×11=7.16小时.
【解析】(1)利用频率分布直方图能求出100名学生中参加实践活动的时间在6~10小时内的人数.
(2)由频率分布直方图可以看出最高矩形横轴上的中点为7,由此能求出这100名学生参加实践活动时间的众数的估计值;(0.04+0.12+0.15+a+0.05)×2=1,求出a=0.14,即可求出这100名学生参加实践活动时间的中位数和平均数。
【考点精析】掌握频率分布直方图是解答本题的根本,需要知道频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.

练习册系列答案
相关题目