题目内容
已知正方形ABCD的边长为2,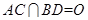 ,
,
将正方形ABCD沿对角线BD折起,使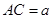 ,得到三棱锥
,得到三棱锥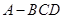 ,如图所示。
,如图所示。
(1)当a=2时,求证: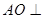 平面BCD;
平面BCD;
(2)当二面角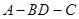 的大小为
的大小为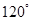 时,
时,
求二面角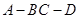 的正切值。
的正切值。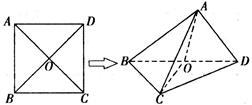
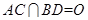 ,
,将正方形ABCD沿对角线BD折起,使
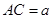 ,得到三棱锥
,得到三棱锥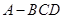 ,如图所示。
,如图所示。(1)当a=2时,求证:
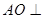 平面BCD;
平面BCD;(2)当二面角
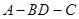 的大小为
的大小为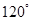 时,
时,求二面角
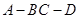 的正切值。
的正切值。
(1)见解析;(2) .
.
 .
.本试题主要考查了立体几何中的二面角的求解线面垂直的证明。
(1)证明:根据题意,在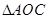 中,
中,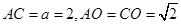 ,
,
所以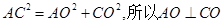 2分
2分
因为AC、BD是正方形ABCD的对角线,所以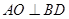
因为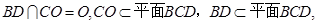 所以
所以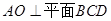 4分
4分
(2)解:由(1)知,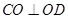 ,以O为原点,OC,OD所在的直线分别为x轴,y轴建立如图所示的空间直角坐标系O-xyz,则
,以O为原点,OC,OD所在的直线分别为x轴,y轴建立如图所示的空间直角坐标系O-xyz,则
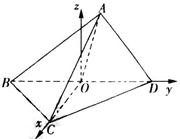
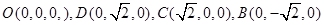 .
.
设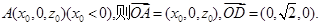 6分
6分
又设平面ABD的法向量为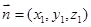 ,
,
则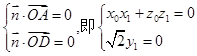
所以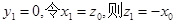 所以
所以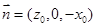 8分
8分
因为平面BCD的一个法向量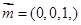 且二面角A-BD-C的大小为
且二面角A-BD-C的大小为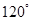 ,
,
所以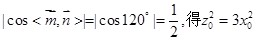 ,因为
,因为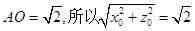
解得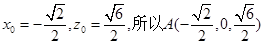 。 9分
。 9分
设平面ABC的法向量为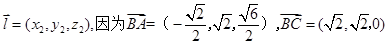
 令
令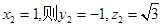
所以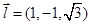 10分
10分
设二面角A-BC-D的平面角为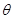 ,
,
所以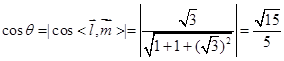 所以
所以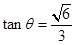
所以二面角A-BC-D的正切值为 . 12分
. 12分
(1)证明:根据题意,在
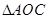 中,
中,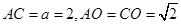 ,
,所以
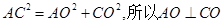 2分
2分因为AC、BD是正方形ABCD的对角线,所以
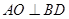
因为
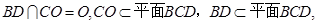 所以
所以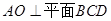 4分
4分(2)解:由(1)知,
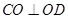 ,以O为原点,OC,OD所在的直线分别为x轴,y轴建立如图所示的空间直角坐标系O-xyz,则
,以O为原点,OC,OD所在的直线分别为x轴,y轴建立如图所示的空间直角坐标系O-xyz,则
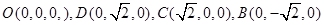 .
.设
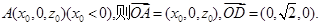 6分
6分又设平面ABD的法向量为
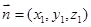 ,
,则
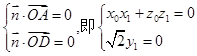
所以
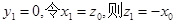 所以
所以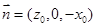 8分
8分因为平面BCD的一个法向量
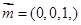 且二面角A-BD-C的大小为
且二面角A-BD-C的大小为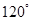 ,
,所以
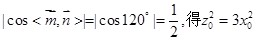 ,因为
,因为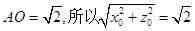
解得
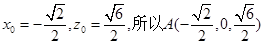 。 9分
。 9分设平面ABC的法向量为
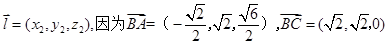
 令
令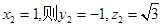
所以
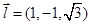 10分
10分设二面角A-BC-D的平面角为
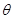 ,
,所以
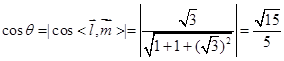 所以
所以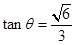
所以二面角A-BC-D的正切值为
 . 12分
. 12分
练习册系列答案
相关题目
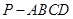 中,
中,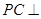 底面
底面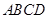 ,
,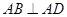 ,
,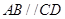 ,
,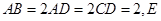 是
是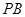 的中点。
的中点。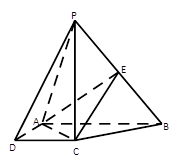
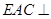 平面
平面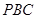 (4分)
(4分)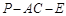 的余弦值为
的余弦值为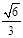 ,求直线
,求直线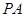 与平面
与平面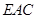 所成角的正弦值.(8分)
所成角的正弦值.(8分)
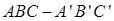 中,
中,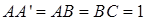 ,
,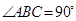 .棱
.棱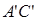 上有两个动点E,F,且EF = a (a为常数).
上有两个动点E,F,且EF = a (a为常数).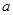
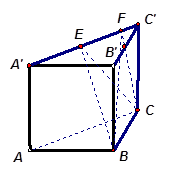
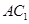 的长、宽、高分别为3、2、1,则从A到
的长、宽、高分别为3、2、1,则从A到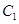 沿长方体的表面的最短距离为( )
沿长方体的表面的最短距离为( )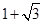
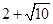
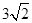
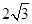
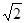 ,则球O的表面积为( )
,则球O的表面积为( )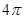 B、
B、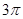 C、
C、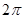 D、
D、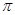
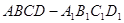 中,
中, 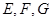 是
是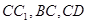 的中点
的中点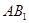 ∥平面
∥平面 ;
;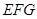 ∥平面
∥平面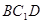
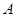 为端点的三条棱长都等于1,且它们彼此的夹角都是
为端点的三条棱长都等于1,且它们彼此的夹角都是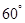 ,那么以这个顶点为端点的晶体的对角线的长为 。
,那么以这个顶点为端点的晶体的对角线的长为 。