题目内容
已知等腰直角三角形ABC中，∠B=90°，AC，BC的中点分别是D，E，将△CDE沿DE折起，使得C-DE-A为直二面角，此时斜边AC被折成折线ADC，则∠ADC等于（ ）
分析：设等腰△ABC中，AB=BC=2，由∠B=90°，AC，BC的中点分别是D，E，知AD=DC=
，DE=CE=1，∠DEC=90°，AE=
，由C-DE-A为直二面角，知∠AEC=90°，AC=
，由此利用余弦定理能求出∠ADC的大小．
| 2 |
| 5 |
| 6 |
解答：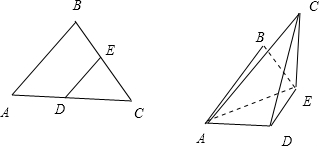
解：如图，设等腰△ABC中，AB=BC=2，
∵∠B=90°，AC，BC的中点分别是D，E，
∴AD=DC=
，DE=CE=1，∠DEC=90°，AE=
，
∵将△CDE沿DE折起，使得C-DE-A为直二面角，
∴∠AEC=90°，AC=
=
，
∴cos∠ADC=
=
=-
，
∴∠ADC=120°，
故选C．
解：如图，设等腰△ABC中，AB=BC=2，∵∠B=90°，AC，BC的中点分别是D，E，
∴AD=DC=
| 2 |
| 5 |
∵将△CDE沿DE折起，使得C-DE-A为直二面角，
∴∠AEC=90°，AC=
| 5+1 |
| 6 |
∴cos∠ADC=
| AD2+DC2-AC2 |
| 2AD•DC |
| 2+2-6 | ||||
2×
|
| 1 |
| 2 |
∴∠ADC=120°，
故选C．
点评：本题以等腰直角三角形的翻折问题为载体，考查空间角的求法，解题时要认真审题，注意翻折前后常量与变量的相互关系的合理运用．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
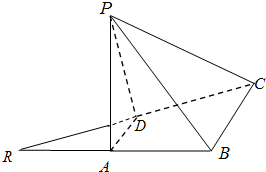如图，已知等腰直角三角形RBC，其中∠RBC=90°，RB=BC=2．点A、D分别是RB、RC的中点，现将△RAD沿着边AD折起到△PAD位置，使PA⊥AB，连接PB、PC．
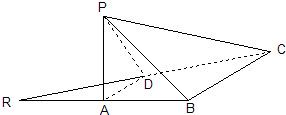如图，已知等腰直角三角形RBC，其中∠RBC=90°，RB=BC=2．点A、D分别是RB、RC的中点，现将△RAD沿着边AD折起到△PAD位置，使PA⊥AB，连接PB、PC．