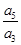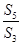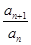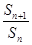题目内容
已知等比数列{an}的公比为q,记bn=am(n-1)+1+am(n-1)+2+…+am(n-1)+m,cn=am(n-1)+1·am(n-1)+2·…·am(n-1)+m(m,n∈N*),则以下结论一定正确的是( )
| A.数列{bn}为等差数列,公差为qm |
| B.数列{bn}为等比数列,公比为q2m |
| C.数列{cn}为等比数列,公比为qm2 |
| D.数列{cn}为等比数列,公比为qmm |
C
解析

练习册系列答案
相关题目
设 成等比数列,其公比为2,则
成等比数列,其公比为2,则 的值为( )
的值为( )
A. | B. | C. | D.1 |
一个等比数列的第3项和第4项分别是12和18,则它的第2项为( )
| A.4 | B.8 | C. | D. |
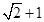 与
与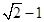 ,两数的等比中项是( )
,两数的等比中项是( )
A.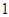 | B.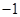 | C. | D.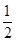 |
设等比数列{an}的各项均为正数,公比为q,前n项和为Sn.若对?n∈N*,有S2n<3Sn,则q的取值范围是( )
| A.(0,1] | B.(0,2) | C.[1,2) | D.(0, ) ) |
一个由正数组成的等比数列,它的前4项和是前2项和的5倍,则此数列的公比为( )
| A.1 | B.2 | C.3 | D.4 |
设首项为1,公比为 的等比数列{an}的前n项和为Sn,则 ( ).
的等比数列{an}的前n项和为Sn,则 ( ).
| A.Sn=2an-1 | B.Sn=3an-2 |
| C.Sn=4-3an | D.Sn=3-2an |
 的前5项和为( )
的前5项和为( )