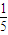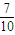题目内容
在正方体AC1中,E是CD的中点,连接AE并延长与BC的延长线交于点F,连接BE并延长交AD的延长线于点G,连接FG.求证:直线FG?平面ABCD且直线FG∥直线A1B1.
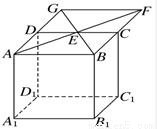
【答案】分析:分别说明点F与点G在平面ABCD内,结合公理一直线上有两点在平面内则这条直线就在这个平面内,易证四边形CFGD是平行四边形,结合棱柱的结构特征,即可求出直线FG∥直线A1B1.
解答:证明:由已知得E是CD的中点,
在正方体中,有A∈平面ABCD,
E∈平面ABCD,
所以AE?平面ABCD.
又AE∩BC=F,所以F∈AE,
从而F∈平面ABCD.
同理,G∈平面ABCD,
所以FG?平面ABCD.
因为EC AB,故在Rt△FBA中,CF=BC,
AB,故在Rt△FBA中,CF=BC,
同理,DG=AD.又在正方形ABCD中,BC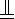 AD,
AD,
所以CF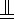 DG.
DG.
所以四边形CFGD是平行四边形.
所以FG∥CD.又CD∥AB,AB∥A1B1,
所以直线FG∥直线A1B1.
点评:本题主要考查了空间中直线与直线之间的位置关系,以及棱柱的结构特征,属于基础题.
解答:证明:由已知得E是CD的中点,
在正方体中,有A∈平面ABCD,
E∈平面ABCD,
所以AE?平面ABCD.
又AE∩BC=F,所以F∈AE,
从而F∈平面ABCD.
同理,G∈平面ABCD,
所以FG?平面ABCD.
因为EC
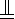 AB,故在Rt△FBA中,CF=BC,
AB,故在Rt△FBA中,CF=BC,同理,DG=AD.又在正方形ABCD中,BC
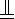 AD,
AD,所以CF
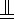 DG.
DG.所以四边形CFGD是平行四边形.
所以FG∥CD.又CD∥AB,AB∥A1B1,
所以直线FG∥直线A1B1.
点评:本题主要考查了空间中直线与直线之间的位置关系,以及棱柱的结构特征,属于基础题.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
在正方体AC1中,E、F分别为AB和CD的中点,则异面直线A1E与BF所成角的余弦值为( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
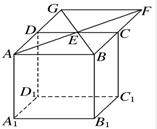 在正方体AC1中,E是CD的中点,连接AE并延长与BC的延长线交于点F,连接BE并延长交AD的延长线于点G,连接FG.
在正方体AC1中,E是CD的中点,连接AE并延长与BC的延长线交于点F,连接BE并延长交AD的延长线于点G,连接FG.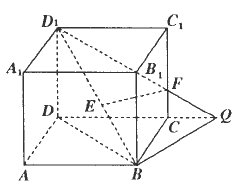
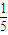
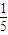
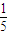 或
或