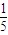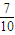题目内容
在正方体AC1中,E、F分别为AB和CD的中点,则异面直线A1E与BF所成角的余弦值为( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
分析:要求两条异面直线所成的角,根据正方形的性质作出ED,则完成了直线的平移,把两条异面直线放到具有公共点的位置,得到两条异面直线所成的角,在三角形中利用余弦定理得到结果.
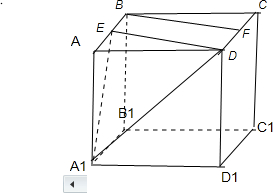
解答:解:连接ED,由正方体的性质知BF∥DE,
∴异面直线A1E与BF所成角是∠A1ED,
设正方体的棱长是1,
∴A1D=
,A1E=ED=
,
∴由余弦定理知cos∠A1ED=
=
故选B.
∴异面直线A1E与BF所成角是∠A1ED,
设正方体的棱长是1,
∴A1D=
| 2 |
|
∴由余弦定理知cos∠A1ED=
| ||||||||
2×
|
| 1 |
| 5 |

故选B.
点评:本题考查异面直线所成的角,本题是一个典型的题目,通过平移得到角,在一个可解的三角形中求出角,按照一画二证三求的过程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
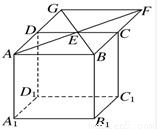
 在正方体AC1中,E是CD的中点,连接AE并延长与BC的延长线交于点F,连接BE并延长交AD的延长线于点G,连接FG.
在正方体AC1中,E是CD的中点,连接AE并延长与BC的延长线交于点F,连接BE并延长交AD的延长线于点G,连接FG.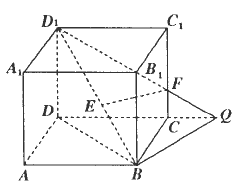
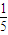
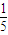
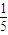 或
或