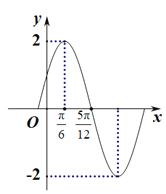
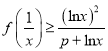题目内容
【题目】2020年春节突如其来的新型冠状病毒肺炎在湖北爆发,为了打赢疫情防控阻击战,我们执行了延长假期政策,在延长假期面前,我们“停课不停学”,河南省教育厅组织部分优秀学校的优秀教师录播《名师同步课堂》,我校高一年级要在甲、乙、丙、丁、戊5位数学教师中随机抽取3人参加录播课堂,则甲、乙两位教师同时被选中的概率为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
(方法一)结合组合数,直接根据古典概型的概率计算公式求解即可.
(方法二)利用列举法,直接根据古典概型的概率计算公式求解即可.
解:(方法一)由题意得,甲、乙两位教师同时被选中的概率为![]() ,
,
(方法二)将甲、乙、丙、丁、戊5位数学教师依次编号为![]() ,
,
记“甲、乙两位教师同时被选中” 为事件![]() ,
,
从5位数学教师中随机抽取3人有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共10种情况,
共10种情况,
事件![]() 包含
包含![]() ,
,![]() ,
,![]() 共3种情况,
共3种情况,
∴![]() ,
,
故选:A.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况,在本市的所有中学生中随机抽取了120名学生进行调查,现将日均自学时间小于1小时的学生称为“自学不足”者![]() 根据调查结果统计后,得到如下
根据调查结果统计后,得到如下![]() 列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为
列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为![]() .
.
非自学不足 | 自学不足 | 合计 | |
配有智能手机 | 30 | ||
没有智能手机 | 10 | ||
合计 |
![]() 请完成上面的列联表;
请完成上面的列联表;
![]() 根据列联表的数据,能否有
根据列联表的数据,能否有![]() 的把握认为“自学不足”与“配有智能手机”有关?
的把握认为“自学不足”与“配有智能手机”有关?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|