题目内容
已知z1,z2是复数,求证:若|z1-. | z2 |
分析:利用|z|2=z•
,结合|z1-
|=|1-z1z2|的平方,化简出|z1|2+|z2|2=1+|z1|2•|z2|2.
通过分解因式,推出|z1|,|z2|中至少有一个值为1.
. |
| z |
. |
| z2 |
通过分解因式,推出|z1|,|z2|中至少有一个值为1.
解答:证:∵|z1-
|=|1-z1z2|
∴|z1-
|2=|1-z1z2|2.
∴(z1-
)
=(1-z1z2)
.
∴(z1-
)(
-z2)=(1-z1z2)(1-
).
化简后得z1
+z2
=1+z1z2
.
∴|z1|2+|z2|2=1+|z1|2•|z2|2.
∴(|z1|2-1)(|z2|2-1)=0.∴|z1|2=1,或|z2|2=1.
∴|z1|,|z2|中至少有一个为1.
. |
| z2 |
∴|z1-
. |
| z2 |
∴(z1-
. |
| z2 |
. | ||
(z1-
|
. |
| (1-z1z2) |
∴(z1-
. |
| z2 |
. |
| z1 |
. |
| z1 |
. |
| z2 |
化简后得z1
. |
| z1 |
. |
| z2 |
. |
| z1 |
. |
| z2 |
∴|z1|2+|z2|2=1+|z1|2•|z2|2.
∴(|z1|2-1)(|z2|2-1)=0.∴|z1|2=1,或|z2|2=1.
∴|z1|,|z2|中至少有一个为1.
点评:本题考查复数的基本概念,复数代数形式的乘除运算,考查转化思想,计算能力,是基础题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
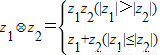 若z1=2+i且z1?z2=3+4i,则复数z2=( )
若z1=2+i且z1?z2=3+4i,则复数z2=( )