题目内容
已知z1,z2是复数,定义复数的一种运算“?”为:z1?z2=
若z1=2+i且z1?z2=3+4i,则复数z2=( )
|
分析:题目给出了一种新运算,并且给出了复数z1和运算后的结果,我们可以运用反证法证题的思想,先假设是其中的一种运算,然后根据这种运算求出z2,看是否满足这种运算成立的条件,若满足,则保留运算结果,否则,则舍掉这种运算结果.
解答:解:由z1=2+i且z1?z2=3+4i,
若|z1|>|z2|,根据给出的定义运算,则z2=
=
=
=2+i
此时|z1|=|z2|=
=
,与|z1|>|z2|矛盾.
若|z1|≤|z2|,根据给出的定义运算,则z2=(3+4i)-(2+i)=1+3i.
此时|z1|=
,|z2|=
=
,符合|z1|≤|z2|.
所以,复数z2=1+3i.
故选B.
若|z1|>|z2|,根据给出的定义运算,则z2=
| 3+4i |
| 2+i |
| (3+4i)(2-i) |
| (2+i)(2-i) |
| 10+5i |
| 5 |
此时|z1|=|z2|=
| 22+12 |
| 5 |
若|z1|≤|z2|,根据给出的定义运算,则z2=(3+4i)-(2+i)=1+3i.
此时|z1|=
| 5 |
| 12+32 |
| 10 |
所以,复数z2=1+3i.
故选B.
点评:本题是在新定义下考查复数代数形式的混合运算,考查了逆向思维和反证法解题的思想,是基础题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
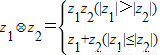 若z1=2+i且z1?z2=3+4i,则复数z2=( )
若z1=2+i且z1?z2=3+4i,则复数z2=( )