题目内容
(1)已知Z是复数,求证:①|Z|2=Z•
;②
=
-Z;
(2)已知z1,z2是复数,若|z1-
|=|1-z1z2|,求证:|z1|,|z2|中至少有一个值为1.
. |
| Z |
. | ||
Z-
|
. |
| Z |
(2)已知z1,z2是复数,若|z1-
. |
| z2 |
分析:(1)设 z=a+bi,a、b∈R,分别代入两个等式的左右两边化简,即可证得等式成立.
(2)把已知条件两边平方,利用共轭复数的性质化简可得z1
+z2
=1+z1z2
,可得(|z1|2-1)(|z2|2-1)
=0,从而有|z1|,|z2|中至少有一个为1.
(2)把已知条件两边平方,利用共轭复数的性质化简可得z1
. |
| z1 |
. |
| z2 |
. |
| z1 |
. |
| z2 |
=0,从而有|z1|,|z2|中至少有一个为1.
解答:解:(1)设 z=a+bi,a、b∈R,
∵|Z|2=a2+b2,Z•
=9a+bi)(a-bi)=a2+b2,∴①|Z|2=Z•
成立.
∵
=
=-2bi,
-Z=(a-bi)-(a+bi)=-2bi,∴②
=
-Z成立.
(2)∵|z1-
|=|1-z1z2|,∴|z1-
|2 =|1-z1z2|2 .
∴(z1-
) (
)=(1-z1z2)(1-
).
∴(z1-
)(
-z2)=( 1-z1z2)(1-
).
化简后得z1
+z2
=1+z1z2
.
∴|z1|2+|z2|2=1+|z1|2•|z2|2.∴(|z1|2-1)(|z2|2-1)=0.
∴|z1|2=1,或|z2|2=1.∴|z1|,|z2|中至少有一个为1.
∵|Z|2=a2+b2,Z•
. |
| Z |
. |
| Z |
∵
. | ||
Z-
|
. |
| (a+bi)-(a-bi) |
. |
| Z |
. | ||
Z-
|
. |
| Z |
(2)∵|z1-
. |
| z2 |
. |
| z2 |
∴(z1-
. |
| z2 |
. | ||
z1-
|
. |
| 1-z1z2 |
∴(z1-
. |
| z2 |
. |
| z1 |
. |
| z1 |
. |
| z2 |
化简后得z1
. |
| z1 |
. |
| z2 |
. |
| z1 |
. |
| z2 |
∴|z1|2+|z2|2=1+|z1|2•|z2|2.∴(|z1|2-1)(|z2|2-1)=0.
∴|z1|2=1,或|z2|2=1.∴|z1|,|z2|中至少有一个为1.
点评:本题主要考查共轭复数的定义和性质,两个复数代数形式的乘除法,求复数的模的方法,属于基础题.

练习册系列答案
相关题目
 ;②
;② ;
;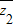 |=|1-z1z2|,求证:|z1|,|z2|中至少有一个值为1.
|=|1-z1z2|,求证:|z1|,|z2|中至少有一个值为1.