题目内容
(本小题满分12分)
(Ⅰ)已知函数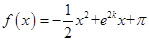 在
在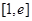 上具有单调性,求实数
上具有单调性,求实数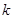 的取值范围;
的取值范围;
(Ⅱ)已知向量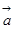 、
、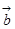 、
、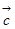 两两所成的角相等,且
两两所成的角相等,且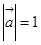 ,
,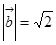 ,
,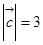 ,求
,求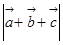 .
.
(Ⅰ)已知函数
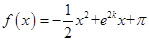 在
在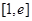 上具有单调性,求实数
上具有单调性,求实数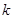 的取值范围;
的取值范围;(Ⅱ)已知向量
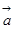 、
、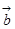 、
、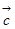 两两所成的角相等,且
两两所成的角相等,且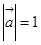 ,
,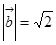 ,
,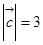 ,求
,求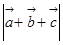 .
.(Ⅰ)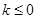 或
或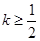 (Ⅱ)
(Ⅱ) 或
或
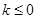 或
或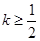 (Ⅱ)
(Ⅱ) 或
或
试题分析:(Ⅰ)因为函数
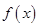 是二次函数,其图象对称轴为
是二次函数,其图象对称轴为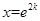
又
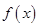 在
在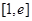 上具有单调性,
上具有单调性,所以
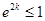 或
或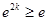 ,
, 解得
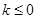 或
或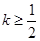 ,
,故实数
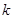 的取值范围是
的取值范围是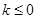 或
或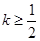 .
. (Ⅱ)当 向量
 两两所成的角为
两两所成的角为 时,
时,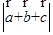 =
=
当 向量
 两两所成的角为
两两所成的角为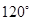 时,
时, =
=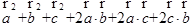
=
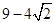
所以
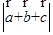 =
=
故
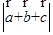 =
= 或
或
点评:第一问中考查二次函数的性质和应用,是基础题.解题的关键是灵活应用二次函数的性质,第二问中主要把握好向量模和数量积间的转化.

练习册系列答案
相关题目

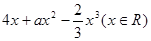 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.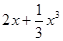 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.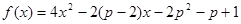 在区间
在区间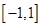 内至少存在一数值
内至少存在一数值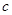 ,使
,使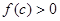 ,则实数
,则实数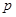 的取值范围是______________________.
的取值范围是______________________. 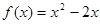 ,
,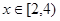 ,则
,则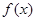 的值域是___________
的值域是___________ 在
在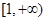 单调递增,则
单调递增,则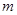 的取值范围为 。
的取值范围为 。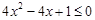 的解集是
的解集是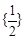
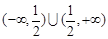
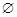
 的零点个数为
的零点个数为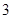 ,则
,则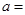 __ __ _
__ __ _