题目内容
在直三棱柱中,AA1=AB=BC=3,AC=2,D是AC的中点.
(1)求证:B1C∥平面A1BD;
(2)求平面A1DB与平面DBB1夹角的余弦值.
(1)详见解析;(2)平面A1DB与平面DBB1夹角的余弦值为 .
.
解析试题分析:(1)求证: 平面
平面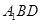 ;利用线面平行的判定定理,证明线面平行,即证线线平行,可利用三角形的中位线,或平行四边形的对边平行,本题由于
;利用线面平行的判定定理,证明线面平行,即证线线平行,可利用三角形的中位线,或平行四边形的对边平行,本题由于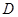 是
是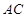 的中点,可连接
的中点,可连接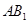 交
交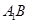 与点
与点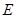 ,连接
,连接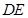 ,利用三角形中位线的性质,证明线线平行即可;(2)求平面
,利用三角形中位线的性质,证明线线平行即可;(2)求平面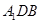 与平面
与平面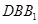 夹角的余弦值,取
夹角的余弦值,取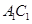 中点
中点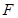 ,则
,则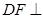 平面
平面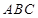 ,则
,则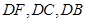 两两垂直,以
两两垂直,以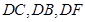 分别为
分别为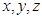 轴建立空间直角坐标系,写出各点的坐标,求出平面
轴建立空间直角坐标系,写出各点的坐标,求出平面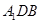 的法向量、平面
的法向量、平面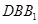 的法向量,利用向量的夹角公式,即可求解.
的法向量,利用向量的夹角公式,即可求解.
试题解析:(1)连接AB1交A1B与点E,连接DE,则B1C∥DE,则B1C∥平面A1BD4分
(2)取A1C1中点F,D为AC中点,则DF⊥平面ABC,
又AB=BC,∴BD⊥AC,∴DF、DC、DB两两垂直,
建立如图所示空间直线坐标系D-xyz,则D(0,0,0), B(0,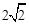 ,0),A1(-1,0,3)
,0),A1(-1,0,3)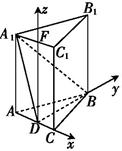
设平面A1BD的一个法向量为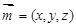 ,
,
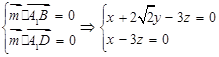
取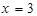 ,则
,则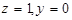 ,
,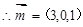 8分
8分
设平面A1DB与平面DBB1夹角的夹角为θ,平面DBB1的一个法向量为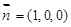 , 10分
, 10分
则
∴平面A1DB与平面DBB1夹角的余弦值为 . 12分
. 12分
考点:用空间向量求平面间的夹角;直线与平面平行的判定;二面角的平面角及求法.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
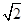 ,E为DC的中点,将它沿AE折成直二面角D-AE-B.
,E为DC的中点,将它沿AE折成直二面角D-AE-B.
 .
.
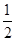 BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).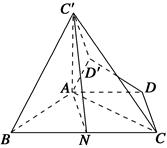
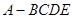 中,
中, 是正三角形,四边形
是正三角形,四边形 是矩形,且平面
是矩形,且平面 平面
平面 ,
, .
.
 是
是 的中点,求证:
的中点,求证: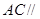 平面
平面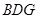 ;
;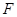 在线段
在线段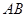 上什么位置时,二面角
上什么位置时,二面角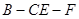 的余弦值为
的余弦值为 .
.
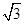 的正三角形,点S在底面ABC上的射影O恰是AC的中点,侧棱SB和底面成45°角.
的正三角形,点S在底面ABC上的射影O恰是AC的中点,侧棱SB和底面成45°角.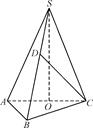
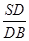 为何值时,CD⊥AB;
为何值时,CD⊥AB;