题目内容
计算下列定积分
(1) |sinx|dx;(2)
|sinx|dx;(2) |x2-1|dx.
|x2-1|dx.
(1)
 |sinx|dx;(2)
|sinx|dx;(2) |x2-1|dx.
|x2-1|dx.(1)4(2)2
(1)∵(-cosx)′=sinx,
∴ |sinx|dx=
|sinx|dx= |sinx|dx+
|sinx|dx+ |sinx|dx
|sinx|dx
= sinxdx-
sinxdx- sinxdx=-cosx|
sinxdx=-cosx| +cosx|
+cosx|
=-(cos -cos0)+(cos2
-cos0)+(cos2 -cos
-cos )=4.
)=4.
(2)∵0≤x≤2,于是|x2-1|=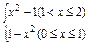
∴ |x2-1|dx=
|x2-1|dx= (1-x2)dx+
(1-x2)dx+ (x2-1)dx
(x2-1)dx
= |
|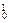 +(
+( x3-x)|
x3-x)|
=(1- )+(
)+( ×23-2)-(
×23-2)-( -1)=2.
-1)=2.
∴
 |sinx|dx=
|sinx|dx= |sinx|dx+
|sinx|dx+ |sinx|dx
|sinx|dx=
 sinxdx-
sinxdx- sinxdx=-cosx|
sinxdx=-cosx| +cosx|
+cosx|
=-(cos
 -cos0)+(cos2
-cos0)+(cos2 -cos
-cos )=4.
)=4.(2)∵0≤x≤2,于是|x2-1|=
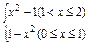
∴
 |x2-1|dx=
|x2-1|dx= (1-x2)dx+
(1-x2)dx+ (x2-1)dx
(x2-1)dx=
 |
|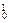 +(
+( x3-x)|
x3-x)|
=(1-
 )+(
)+( ×23-2)-(
×23-2)-( -1)=2.
-1)=2.
练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 ,且
,且 ,求证:
,求证: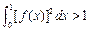 .
. ,宽为2的矩形
,宽为2的矩形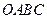 内,曲线
内,曲线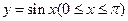 与
与 轴围成如图所示的阴影部分,向矩形
轴围成如图所示的阴影部分,向矩形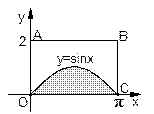
 B.
B.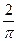 C.
C. 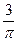 D.
D. 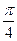
 等于
等于
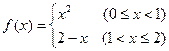 则
则 =( )
=( )

