题目内容
(本题满分14分) 设{an}是由正数组成的等差数列,Sn是其前n项和
(1)若 ,求
,求 的值;
的值;
(2)若互不相等正整数p,q,m,使得p+q=2m,证明:不等式 成立;
成立;
(3)是否存在常数k和等差数列{an},使 恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
【答案】
解:在等差数列{an}中,Sn,S2n-Sn,S3n-S2n,…成等差数列,
∴Sn+(S3n-S2n)=2(S2n-Sn)
∴S3n=3 S2n-3 Sn=60…………………………………………………………………4分
(2)SpSq=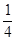 pq(a1+ap)(a1+aq)
pq(a1+ap)(a1+aq)
=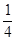 pq[a
pq[a +a1(ap+aq)+apaq]
+a1(ap+aq)+apaq]
=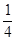 pq(a
pq(a +2a1am+apaq)<
+2a1am+apaq)<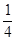 (
( )2[a
)2[a +2a1am+(
+2a1am+(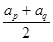 )2]
)2]
=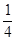 m2(a
m2(a +2a1am+a
+2a1am+a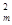 )=[
)=[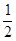 m(a1+am)]2
m(a1+am)]2
=S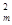 ………………………………………………………………………8分
………………………………………………………………………8分
(3)设an=pn+q(p,q为常数),则ka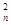 -1=kp2n2+2kpqn+kq2-1
-1=kp2n2+2kpqn+kq2-1
Sn+1=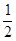 p(n+1)2+
p(n+1)2+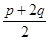 (n+1)
(n+1)
S2n=2pn2+(p+2q)n
∴S2n-Sn+1=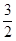 pn2+
pn2+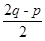 n-(p+q),
n-(p+q),
依题意有kp2n2+2kpqn+kq2-1=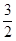 pn2+
pn2+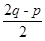 n-(p+q)对一切正整数n成立,
n-(p+q)对一切正整数n成立,
∴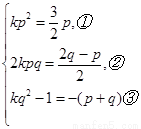
由①得,p=0或kp=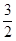 ;
;
若p=0代入②有q=0,而p=q=0不满足③,
∴p≠0
由kp=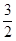 代入②,
代入②,
∴3q=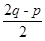 ,q=-
,q=- 代入③得,
代入③得,
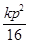 -1=-(p-
-1=-(p- ),将kp=
),将kp=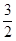 代入得,∴P=
代入得,∴P=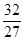 ,
,
解得q=-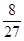 ,k=
,k=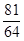
故存在常数k=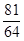 及等差数列an=
及等差数列an=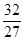 n-
n-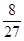 使其满足题意…………………13分
使其满足题意…………………13分
【解析】略

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).