题目内容
过点B（0，-b）作椭圆
+
=1（a＞b＞0）的弦，若弦长的最大值是2b，则椭圆离心率的取值范围是 ．
| x2 |
| a2 |
| y2 |
| b2 |
考点：椭圆的简单性质
专题：计算题,直线与圆,圆锥曲线的定义、性质与方程
分析：讨论过点B的弦斜率不存在和存在时的直线方程，求出交点和弦长，令它不大于2b恒成立，化简整理，得到
2a2b2-a4≥0，运用a，b，c的关系和离心率公式，即可得到范围．
2a2b2-a4≥0，运用a，b，c的关系和离心率公式，即可得到范围．
解答：
解：若过点B（0，-b）的弦的斜率不存在，则弦长为2b，
若弦的斜率存在，则设弦的方程为：y=kx-b，代入椭圆方程，
得到，（b2+a2k2）x2-2ka2bx=0，解得，x=0或
，
即有交点为（0，-b），（
，
）
则弦长为：
=
≤2b恒成立，
即有a4k2+a4k4≤b4+a4k4+2a2b2k2，即有b4+k2（2a2b2-a4）≥0恒成立，
则2a2b2-a4≥0，即2b2≥a2即有2a2-2c2≥a2，a2≥2c2
即有e=
≤
，
则离心率的范围为：（0，
]．
故答案为：（0，
]
若弦的斜率存在，则设弦的方程为：y=kx-b，代入椭圆方程，
得到，（b2+a2k2）x2-2ka2bx=0，解得，x=0或
| 2ka2b |
| b2+a2k2 |
即有交点为（0，-b），（
| 2ka2b |
| b2+a2k2 |
| k2a2b-b3 |
| b2+a2k2 |
则弦长为：
|
2a2b
| ||
| b2+a2k2 |
即有a4k2+a4k4≤b4+a4k4+2a2b2k2，即有b4+k2（2a2b2-a4）≥0恒成立，
则2a2b2-a4≥0，即2b2≥a2即有2a2-2c2≥a2，a2≥2c2
即有e=
| c |
| a |
| ||
| 2 |
则离心率的范围为：（0，
| ||
| 2 |
故答案为：（0，
| ||
| 2 |
点评：本题考查椭圆的方程和性质，考查直线方程和椭圆方程联立，消去未知数，求出交点，考查运算能力，属于中档题．
练习册系列答案
相关题目
设全集U={x∈N*|x＜6}，集合A={1，3}，∁UB={3，5}，则A∩B=（ ）
| A、{1} | B、{1，5} |
| C、{4} | D、{2} |
设a、b∈R，已知命题p：a2+b2≤2ab，命题q：（
）2≤
，p是q成立的（ ）
| a+b |
| 2 |
| a2+b2 |
| 2 |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
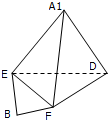如图，边长为2的正方形ABCD中，E是AB边上的点，F是边BC上的点，且BE=BF，若将△AED、△DCF分别沿DE、DF折起，使A、C两点重合于点A1．