题目内容
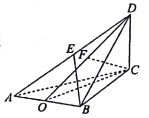
【题目】[2018·郴州期末]已知三棱锥![]() 中,
中,![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,
,![]() 是面积为
是面积为![]() 的等边三角形,
的等边三角形,![]() ,
,![]() ,
,![]() 平面
平面![]() ,垂足为
,垂足为![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:
(1)要证线面垂直,一般先证线线垂直,这可由![]() 和
和![]() 是等边三角形及O是AB中点易得;
是等边三角形及O是AB中点易得;
(2)要求直线与平面所成的角,一种方法作出线面角的平面角,然后解三角形得结论,也可建立空间直角坐标系,如解析中的坐标系,写出各点坐标,求出直线的方向向量与平面的法向量,由方向向量与法向量的夹角与直线和平面所成角互余可得.
试题解析:
(1)证明:∵![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() 是等边三角形.
是等边三角形.
又![]() 是等边三角形.
是等边三角形.
∴![]() 是
是![]() 中点,
中点,![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)解:由(1)知![]() ,平面
,平面![]() 平面
平面![]() .
.
因为平面![]() 与平面
与平面![]() 的交线为
的交线为![]() .
.
∵![]() 平面
平面![]() .∴
.∴![]() .
.
又等边![]() 面积为
面积为![]() ,∴
,∴![]()
又![]() ,∴
,∴ ![]() 是
是![]() 中点.
中点.
如图建立空间直角坐标系![]() ,
,
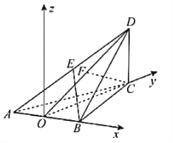
![]() ,
,![]() ,
,![]() ,
,![]()
所以![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则
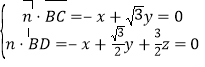 ,取
,取![]() ,则
,则![]() ,
,![]() .
.
即平面![]() 的一个法向量为
的一个法向量为![]() .
.
所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为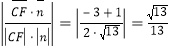 .
.

【题目】某地公共电汽车和地铁按照里程分段计价,具体如下表:
乘公共电汽车方案 | 10公里(含)内2元; 10公里以上部分,每增加1元可乘坐5公里(含) |
乘坐地铁方案 | 6公里(含)内3元; 6公里至12公里(含)4元; 12公里至22公里(含)5元; 22公里至32公里(含)6元; 32公里以上部分,每增加1元可乘坐20公里(含) |
已知在一号线地铁上,任意一站到![]() 站的票价不超过5元,现从那些只乘坐一号线地铁,且在
站的票价不超过5元,现从那些只乘坐一号线地铁,且在![]() 站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.
站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.
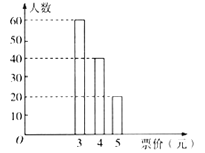
(Ⅰ)如果从那些只乘坐一号线地铁,且在![]() 站出站的乘客中任选1人,试估计此人乘坐地铁的票价小于5元的概率;
站出站的乘客中任选1人,试估计此人乘坐地铁的票价小于5元的概率;
(Ⅱ)已知选出的120人中有6名学生,且这6名学生中票价为3、4、5元的人数分别为3,2,1人,现从这6人中随机选出2人,求这2人的票价和恰好为8元的概率;
(Ⅲ)小李乘坐一号线地铁从![]() 地到
地到![]() 站的票价是5元,返程时,小李乘坐某路公共电汽车所花交通费也是5元,假设小李往返过程中乘坐地铁和公共电汽车的路程均为
站的票价是5元,返程时,小李乘坐某路公共电汽车所花交通费也是5元,假设小李往返过程中乘坐地铁和公共电汽车的路程均为![]() 公里,试写出
公里,试写出![]() 的取值范围.
的取值范围.
【题目】某校高三课外兴趣小组为了解高三同学高考结束后是否打算观看2018年足球世界杯比赛的情况,从全校高三年级1500名男生、1000名女生中按分层抽样的方式抽取125名学生进行问卷调查,情况如下表:
打算观看 | 不打算观看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中数据b,c;
(2)判断是否有99%的把握认为观看2018年足球世界杯比赛与性别有关;
(3)为了计算“从10人中选出9人参加比赛”的情况有多少种,我们可以发现它与“从10人中选出1人不参加比赛”的情况有多少种是一致的.现有问题:在打算观看2018年足球世界杯比赛的同学中有5名男生、2名女生来自高三(5)班,从中推选5人接受校园电视台采访,请根据上述方法,求被推选出的5人中恰有四名男生、一名女生的概率.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附: 