题目内容
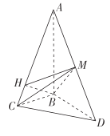
【题目】如图,在三棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,M为
,M为![]() 中点,H为线段
中点,H为线段![]() 上一点(除
上一点(除![]() 的中点外),且
的中点外),且![]() .当三棱锥
.当三棱锥![]() 的体积最大时,则三棱锥
的体积最大时,则三棱锥![]() 的外接球表面积为( )
的外接球表面积为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】B
【解析】
利用线面垂直的判定定理和性质,可以证明![]() 平面
平面![]() ,利用三棱锥的等积性,结合基本不等式,这样可以求出
,利用三棱锥的等积性,结合基本不等式,这样可以求出![]() ,过点C作
,过点C作![]() ,取
,取![]() ,
,![]() 的中点T,N,连接
的中点T,N,连接![]() ,
,![]() ,过点T作
,过点T作![]() 的平行线交
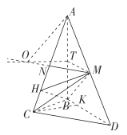
的平行线交![]() 于点O.利用线面垂直的性质和判定定理可以证明出O为三棱锥
于点O.利用线面垂直的性质和判定定理可以证明出O为三棱锥![]() 的外接球的球心,运用正切函数的定义,球的表面积公式进行求解即可.
的外接球的球心,运用正切函数的定义,球的表面积公式进行求解即可.
在![]() 中,因为M为
中,因为M为![]() 中点,故
中点,故![]() ,且
,且![]() ,因为
,因为![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,故
,故![]() ,又因为
,又因为![]() ,所以
,所以![]() 平面
平面![]() ,因此
,因此![]() ,故
,故![]() 平面
平面![]() ,三棱锥
,三棱锥![]() 的体积等于三棱锥
的体积等于三棱锥![]() 的体积,即只需底面
的体积,即只需底面![]() 面积最大即可.因为
面积最大即可.因为![]() ,则
,则![]() ,故
,故![]() ,当且仅当
,当且仅当![]() 时取等号.在
时取等号.在![]() 中,
中,![]() ,故
,故![]() ,过点C作
,过点C作![]() ,取
,取![]() ,
,![]() 的中点T,N,连接
的中点T,N,连接![]() ,
,![]() ,过点T作
,过点T作![]() 的平行线交
的平行线交![]() 于点O.由
于点O.由![]() 平面
平面![]() 知
知![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .因此O为三棱锥
.因此O为三棱锥![]() 的外接球的球心,由
的外接球的球心,由![]() ,因为
,因为![]() ,所以
,所以![]() ,故
,故![]() ,即三棱锥
,即三棱锥![]() 的外接球表面积为
的外接球表面积为![]() .
.
故选:B

 阅读快车系列答案
阅读快车系列答案【题目】在综合素质评价的某个维度的测评中,依据评分细则,学生之间相互打分,最终将所有的数据合成一个分数,满分100分,按照大于或等于80分的为优秀,小于80分的为合格,为了解学生的在该维度的测评结果,在毕业班中随机抽出一个班的数据.该班共有60名学生,得到如下的列联表:
优秀 | 合格 | 总计 | |
男生 | 6 | ||
女生 | 18 | ||
合计 | 60 |
已知在该班随机抽取1人测评结果为优秀的概率为![]() .
.
(1)完成上面的列联表;
(2)能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系?
(3)现在如果想了解全校学生在该维度的表现情况,采取简单随机抽样方式在全校学生中抽取少数一部分来分析,请你选择一个合适的抽样方法,并解释理由.
附: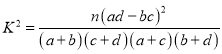
| 0.25 | 0.10 | 0.025 |
| 1.323 | 2.706 | 5.024 |
【题目】我市某区2018年房地产价格因“棚户区改造”实行货币化补偿,使房价快速走高,为抑制房价过快上涨,政府从2019年2月开始采用实物补偿方式(以房换房),3月份开始房价得到很好的抑制,房价渐渐回落,以下是2019年2月后该区新建住宅销售均价的数据:
月份 | 3 | 4 | 5 | 6 | 7 |
价格 | 83 | 82 | 80 | 78 | 77 |
(1)研究发现,3月至7月的各月均价![]() (百元/平方米)与月份
(百元/平方米)与月份![]() 之间具有较强的线性相关关系,求价格
之间具有较强的线性相关关系,求价格![]() (百元/平方米)关于月份
(百元/平方米)关于月份![]() 的线性回归方程;
的线性回归方程;
(2)用![]() 表示用(1)中所求的线性回归方程得到的与
表示用(1)中所求的线性回归方程得到的与![]() 对应的销售均价的估计值,3月份至7月份销售均价估计值
对应的销售均价的估计值,3月份至7月份销售均价估计值![]() 与实际相应月份销售均价
与实际相应月份销售均价![]() 差的绝对值记为
差的绝对值记为![]() ,即
,即![]() ,
,![]() .若
.若![]() ,则将销售均价的数据
,则将销售均价的数据称为一个“好数据”,现从5个销售均价数据中任取2个,求抽取的2个数据均是“好数据”的概率.
参考公式:回归方程系数公式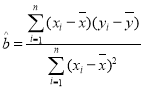 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() .
.