题目内容
14.两同心圆x2+y2=25和x2+y2=16,从外圆上一点作内圆的两条切线,两条切线的夹角为( )| A. | arctan$\frac{4}{3}$ | B. | 2arctan$\frac{4}{3}$ | C. | π-arctan$\frac{4}{3}$ | D. | π-2arctan$\frac{4}{3}$ |
分析 由图可知,两条切线的夹角为∠BAC.由图可求出∠BAO正切值.从而得到两条切线的夹角.
解答 解:如图,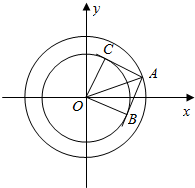
由图可知,|OC|=4,|OA|=5.
∴|AC|=3.
∴tan∠BAO=$\frac{4}{3}$.
∴∠BAO=arctan$\frac{4}{3}$.
又∵∠BAC=2∠BAO,
∴∠BAC=2arctan$\frac{4}{3}$.
∴两条切线的夹角为2arctan$\frac{4}{3}$.
故选:B.
点评 本题考查直线与圆相切的性质,圆与圆的位置关系,三角函数求值等知识的综合应用,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
9.已知物体的运动方程是s=$\frac{1}{3}$t3-4t2+12t(t表示时间,s表示位移),则瞬时速度为0的时刻是( )
| A. | 0秒、2秒或6秒 | B. | 2秒或16秒 | C. | 2秒、8秒或16秒 | D. | 2秒或6秒 |
6.长为2的线段AB的两个端点分别在x轴和y轴上滑动,那么线段AB中点的轨迹是( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
3.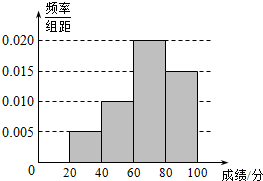 某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )
某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )
 某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )
某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )| A. | 45 | B. | 50 | C. | 55 | D. | 60 |
4.抛物线y=2x2的焦点坐标是( )
| A. | ($\frac{1}{2}$,0) | B. | (-$\frac{1}{2}$,0) | C. | (0,$\frac{1}{8}$) | D. | (0,-$\frac{1}{8}$) |