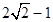题目内容
给定点P(2,-3),Q(3,2),已知直线ax+y+2=0与线段PQ(包括P,Q在内)有公共点,则a的取值范围是______.
设线段PQ上任意一点M(x0,y0),
且令
=t(0≤t≤1),又P(2,-3),Q(3,2),
则x0=(1-t)2+3t=2+t,y0=(1-t)(-3)+t•2=-3+5t,
将x0和y0代入直线ax+y+2=0得:a(2+t)+(-3+5t)+2=0,
解得t=
,
由0≤t≤1得0≤
≤1,
解得:-
≤a≤
,
故答案为:[-
,
]
且令
| PM |
| PQ |
则x0=(1-t)2+3t=2+t,y0=(1-t)(-3)+t•2=-3+5t,
将x0和y0代入直线ax+y+2=0得:a(2+t)+(-3+5t)+2=0,
解得t=
| 1-2a |
| a+5 |
由0≤t≤1得0≤
| 1-2a |
| a+5 |
解得:-
| 4 |
| 3 |
| 1 |
| 2 |
故答案为:[-
| 4 |
| 3 |
| 1 |
| 2 |

练习册系列答案
相关题目
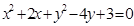 与直线
与直线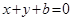 相切,正实数b的值为 ( )
相切,正实数b的值为 ( )