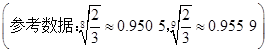题目内容
已知数列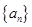 是等差数列,且
是等差数列,且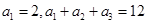 .
.
(1)求数列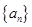 的通项公式;
的通项公式;
(2)令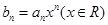 ,求数列
,求数列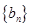 的前
的前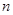 项和.
项和.
(1)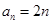 ;(2)当
;(2)当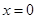 时,
时,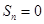 ;当
;当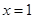 时,
时,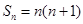 ,当
,当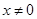 且
且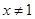 时,
时,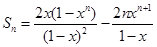 .
.
解析试题分析:(1)利用等差数列的通项公式,将已知的等式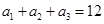 转化成用首项与公差表示,从而求出
转化成用首项与公差表示,从而求出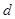 ,最后由等差数列的通项公式
,最后由等差数列的通项公式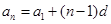 可得到数列
可得到数列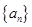 的通项公式;(2)设
的通项公式;(2)设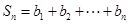 ,从而得到
,从而得到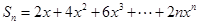 ,针对
,针对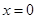 、
、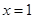 及
及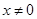 且
且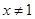 分三类进行求解,当
分三类进行求解,当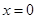 、
、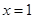 时,直接可求得
时,直接可求得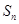 ,当
,当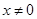 且
且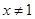 时,应用错位相减法进行求和即可,问题得以解决.
时,应用错位相减法进行求和即可,问题得以解决.
试题解析:(1)设数列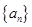 的公差为
的公差为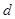 ,则
,则 即
即 ,而
,而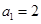 ,所以
,所以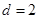
所以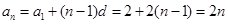
(2)令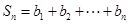 ,其中
,其中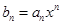
则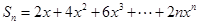 ①
①
当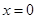 时,
时,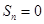
当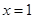 时,
时,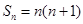
当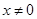 且
且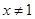 时,
时,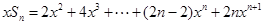 ②
②
①-②得:
∴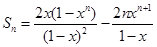 .
.
考点:1.等差数列的通项公式;2.等差数列的前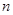 项和公式;3.等比数列的前
项和公式;3.等比数列的前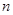 项和公式;4.错位相减法求和;5.分类讨论的思想.
项和公式;4.错位相减法求和;5.分类讨论的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
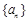 中各项为正数,
中各项为正数,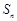 为其前n项和,对任意
为其前n项和,对任意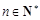 ,总有
,总有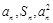 成等差数列.
成等差数列.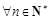 ,
,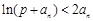 ”是真命题?若存在,求出p;若不存在,请说明理由.
”是真命题?若存在,求出p;若不存在,请说明理由. 为等差数列,且
为等差数列,且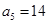 ,
,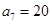 .设数列
.设数列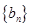 的前
的前 项和为
项和为 ,且
,且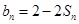 .
.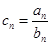 ,
,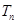 为数列
为数列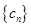 的前
的前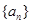 是公比大于
是公比大于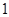 的等比数列,
的等比数列,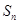 为数列
为数列 项和.已知
项和.已知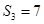 ,且
,且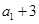 ,
,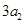 ,
,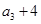 构成等差数列.
构成等差数列.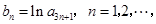 求数列
求数列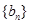 的前
的前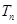 .
.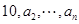 是各项均不为零的
是各项均不为零的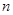 (
(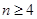 )项等差数列,且公差
)项等差数列,且公差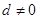 .
. ,且该数列前
,且该数列前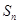 最大,求
最大,求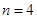 ,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求
,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求 的值;
的值;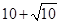 ,则数列
,则数列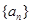 是公差不为0的等差数列,
是公差不为0的等差数列,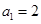 ,且
,且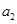 ,
,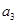 ,
, 成等比数列.
成等比数列.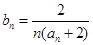 ,求数列
,求数列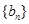 的前
的前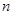 项和
项和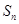 。
。 的前
的前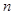 项和为
项和为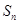 ,且
,且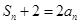 ,数列
,数列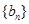 满足
满足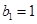 ,且
,且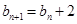 .
.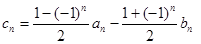 ,求数列
,求数列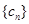 的前
的前 项和
项和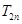 .
.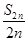 =2013,求n的值;
=2013,求n的值;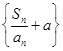 是公比为q(q≠-1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为q=1+
是公比为q(q≠-1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为q=1+ .
.