题目内容
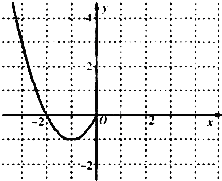 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补完整函数f(x)的图象,并根据图象写出函数f(x)的增区间;
(2)写出函数f(x)的解析式和值域;
(3)若函数f(x)在区间[a,b](a<b)上的值域是[-1,3],则b-a的取值范围是
[2,6]
[2,6]
.分析:(1)根据偶函数的图象关于y轴对称,可作出f(x)的图象,由图象可得f(x)的单调递增区间;
(2)令x>0,则-x<0,根据条件可得f(-x)=x2-2x,利用函数f(x)是定义在R上的偶函数,可得f(x)=f(-x)=x2-2x,从而可得函数f(x)的解析式和值域;
(3)函数f(x)在区间[a,b](a<b)上的值域是[-1,3],确定b-a的最小值与最大值,从而可得b-a的取值范围.
(2)令x>0,则-x<0,根据条件可得f(-x)=x2-2x,利用函数f(x)是定义在R上的偶函数,可得f(x)=f(-x)=x2-2x,从而可得函数f(x)的解析式和值域;
(3)函数f(x)在区间[a,b](a<b)上的值域是[-1,3],确定b-a的最小值与最大值,从而可得b-a的取值范围.
解答: 解:(1)如图,根据偶函数的图象关于y轴对称,可作出f(x)的图象,(2分),则f(x)的单调递增区间为(-1,0),(1,+∞);(5分)
解:(1)如图,根据偶函数的图象关于y轴对称,可作出f(x)的图象,(2分),则f(x)的单调递增区间为(-1,0),(1,+∞);(5分)
(2)令x>0,则-x<0,∴f(-x)=x2-2x
∵函数f(x)是定义在R上的偶函数,
∴f(x)=f(-x)=x2-2x
∴解析式为f(x)=
(8分)
值域为{y|y≥-1}.(10分)
(3)当x≤0时,令f(x)=x2+2x=3,则x=-3
∵函数f(x)在区间[a,b](a<b)上的值域是[-1,3],
∴b-a的最小值为-1+3=2,最大值为3+3=6
∴b-a的取值范围是[2,6](14分)
 解:(1)如图,根据偶函数的图象关于y轴对称,可作出f(x)的图象,(2分),则f(x)的单调递增区间为(-1,0),(1,+∞);(5分)
解:(1)如图,根据偶函数的图象关于y轴对称,可作出f(x)的图象,(2分),则f(x)的单调递增区间为(-1,0),(1,+∞);(5分)(2)令x>0,则-x<0,∴f(-x)=x2-2x
∵函数f(x)是定义在R上的偶函数,
∴f(x)=f(-x)=x2-2x
∴解析式为f(x)=
|
值域为{y|y≥-1}.(10分)
(3)当x≤0时,令f(x)=x2+2x=3,则x=-3
∵函数f(x)在区间[a,b](a<b)上的值域是[-1,3],
∴b-a的最小值为-1+3=2,最大值为3+3=6
∴b-a的取值范围是[2,6](14分)
点评:本题考查函数图象的作法,考查函数解析式的确定与函数的单调性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 已知函数f(x)=x+
已知函数f(x)=x+