题目内容

4．已知函数f（x）的定义域为（0，+∞）且f（x+y）=f（x）+f（y）对一切正实数x、y都成立，若f（8）=4，则f（2）=1．

分析 由f（x+y）=f（x）+f（y）对一切正实数x、y都成立，分别令x=y=4，x=y=2；从而代入求解即可．

解答 解：∵f（x+y）=f（x）+f（y）对一切正实数x、y都成立，
令x=y=4得，f（8）=f（4）+f（4）=4，
故f（4）=2；
令x=y=2得，f（4）=f（2）+f（2）=2，
故f（2）=1；
故答案为：1．

点评 本题考查了抽象函数的应用，注意对f（x+y）=f（x）+f（y）中的x，y赋值．

练习册系列答案
相关题目
14．已知等比数列{an}的前n项和为Sn，则下列一定成立的是（　　）
A．若a3＞0，则a2015＜0B．若a4＞0，则a2015＜0
C．若a3＞0，则a2015＞0D．若a4＞0，则a2015＞0
15．已知数列{an}各项均为正数，且满足a1=1，an+1=2an+1（n∈N*）．
（1）求数列{an}的通项公式an；
（2）若点Pn（an，yn）（n∈N*）是曲线f（x）=$\frac{lo{g}_{2}（x+1）}{x+1}$（x＞0）上的列点，且点Pn（an，yn）在x轴上的射影为Qn（an，0）（n∈N*），设四边形PnQnQn+1Pn+1的面积是Sn，求证：n∈N*时，$\frac{1}{{S}_{1}}$+$\frac{1}{2{S}_{2}}$+$\frac{1}{3{S}_{n}}$+…+$\frac{1}{n{S}_{n}}$＜$\frac{7}{3}$．
12．已知函数f（x）满足f（x+1）=f（x-1），且f（x）是偶函数，当x∈[0，1]时，f（x）=x，若在区间[-1.3]上函数g（x）=f（x）-kx-k有4个零点，求实数k的取值范围．
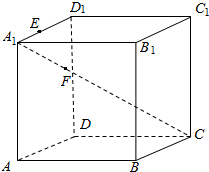19．如图所示，在正方体ABCD-A1B1C1D1中，E在A1D1上，且$\overrightarrow{{A}_{1}E}=2\overrightarrow{E{D}_{1}}$，F在对角线A1C上，且$\overrightarrow{{A}_{1}F}=\frac{2}{3}\overrightarrow{FC}$．求证：E，F，B三点共线．
9．求函数y=sin2x-4cosx+5的值域．
16．三个数学爱好者各自出题给对方做．
甲出的题目是：（1）证明不等式$\frac{x}{1+x}$＜ln（1+x）＜x，x＞0；
乙出的题目是：（2）在数列{an}中，已知a1=$\frac{1}{2}$，且$\frac{{a}_{n}{a}_{n-1}}{{a}_{n-1}-{a}_{n}}$=1+$\frac{1}{n^2-n-1}$，求数列{an}的通项公式an；
丙看完后出的题目是：在（2）中，设数列{an}的前n项和为Sn，证明：-1+lnn＜Sn≤$\frac{1}{2}$+lnn．
13．已知O是坐标原点，F是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的一个焦点，过F且与x轴垂直的直线与椭圆交于M，N两点，则cos∠MON的值为（　　）
A．$\frac{5}{13}$B．-$\frac{5}{13}$C．$\frac{2\sqrt{13}}{13}$D．-$\frac{2\sqrt{13}}{13}$
14．已知F1、F2分别是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，椭圆上一点M满足△MF1F2的周长为4+2$\sqrt{3}$，过椭圆上顶点与右顶点的直线与直线4x-2y+5=0垂直．
（1）求椭圆C的方程；
（2）若直线l交椭圆C于A，B两点，以AB为直径的圆过原点，求弦长|AB|的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网