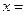题目内容
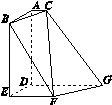
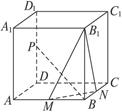
如图,在四棱锥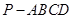 中,
中,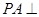 底面
底面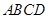 ,
,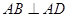 ,
,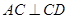 ,
,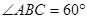
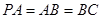 ,
,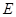 是
是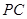 的中点.
的中点.
(Ⅰ)证明: ;
;
(Ⅱ)证明: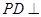 平面
平面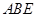 ;
;
(Ⅲ)求二面角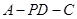 的正切值
的正切值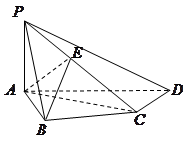
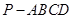 中,
中,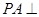 底面
底面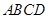 ,
,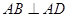 ,
,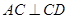 ,
,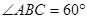
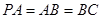 ,
,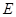 是
是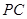 的中点.
的中点.(Ⅰ)证明:
 ;
;(Ⅱ)证明:
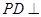 平面
平面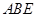 ;
;(Ⅲ)求二面角
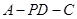 的正切值
的正切值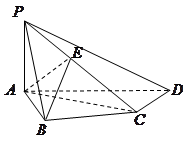
(Ⅰ)证明:在四棱锥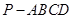 中,因
中,因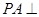 底面
底面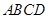 ,
,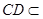 平面
平面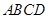 ,故
,故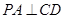 .
.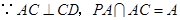 ,
,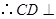 平面
平面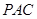 .
.
而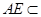 平面
平面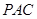 ,
,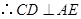 .…………………………………………(4分)
.…………………………………………(4分)
(Ⅱ)证明:由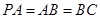 ,
,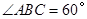 ,可得
,可得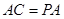 .
.
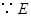 是
是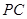 的中点,
的中点,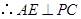 .由(Ⅰ)知,
.由(Ⅰ)知,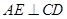 ,且
,且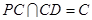 ,所以
,所以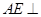 平面
平面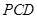 .而
.而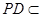 平面
平面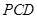 ,
,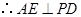 .
.
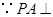 底面
底面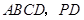 在底面
在底面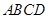 内的射影是
内的射影是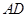 ,
,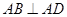 ,
,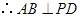 .
.
又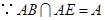 ,综上得
,综上得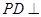 平面
平面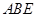 .………………………………(8分)
.………………………………(8分)
(Ⅲ)解法一:过点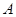 作
作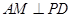 ,垂足为
,垂足为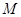 ,连结
,连结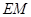 .则(Ⅱ)知,
.则(Ⅱ)知,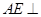 平面
平面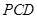 ,
,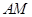 在平面
在平面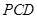 内的射影是
内的射影是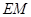 ,则
,则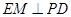 .因此
.因此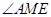 是二面角
是二面角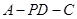 的平面角.由已知,得
的平面角.由已知,得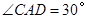 .设
.设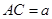 ,
,
可得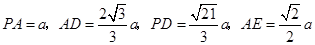 .
.
在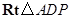 中,
中,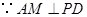 ,
,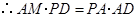 ,
,
则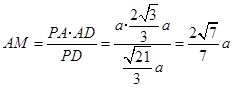 .
.
在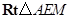 中,
中,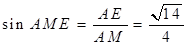 .所以二面角
.所以二面角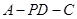 的正切值为
的正切值为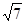 .
.
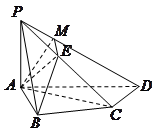
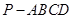 中,因
中,因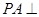 底面
底面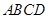 ,
,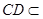 平面
平面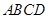 ,故
,故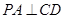 .
.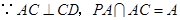 ,
,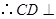 平面
平面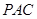 .
.而
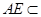 平面
平面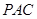 ,
,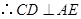 .…………………………………………(4分)
.…………………………………………(4分)(Ⅱ)证明:由
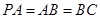 ,
,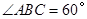 ,可得
,可得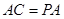 .
.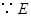 是
是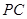 的中点,
的中点,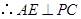 .由(Ⅰ)知,
.由(Ⅰ)知,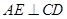 ,且
,且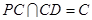 ,所以
,所以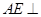 平面
平面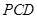 .而
.而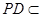 平面
平面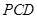 ,
,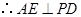 .
.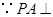 底面
底面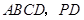 在底面
在底面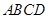 内的射影是
内的射影是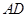 ,
,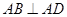 ,
,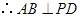 .
.又
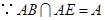 ,综上得
,综上得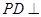 平面
平面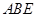 .………………………………(8分)
.………………………………(8分)(Ⅲ)解法一:过点
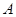 作
作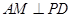 ,垂足为
,垂足为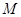 ,连结
,连结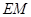 .则(Ⅱ)知,
.则(Ⅱ)知,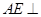 平面
平面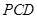 ,
,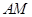 在平面
在平面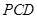 内的射影是
内的射影是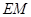 ,则
,则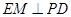 .因此
.因此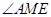 是二面角
是二面角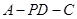 的平面角.由已知,得
的平面角.由已知,得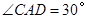 .设
.设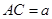 ,
,可得
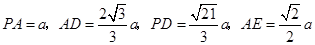 .
.在
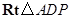 中,
中,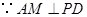 ,
,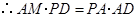 ,
,则
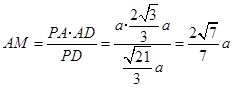 .
.在
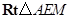 中,
中,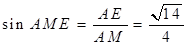 .所以二面角
.所以二面角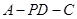 的正切值为
的正切值为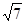 .
.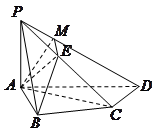
(I)证明: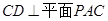 即可.
即可.
(II)分别证明: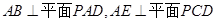 即可.
即可.
(III)可以利用空间向量的知识直接求,也可以直接根据三垂线定理作出二面角的平面角解三角形即可
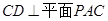 即可.
即可.(II)分别证明:
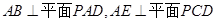 即可.
即可.(III)可以利用空间向量的知识直接求,也可以直接根据三垂线定理作出二面角的平面角解三角形即可

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
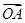 =
=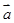 ,
,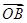 =
=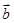 ,其中
,其中 =λ
=λ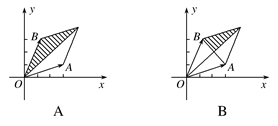
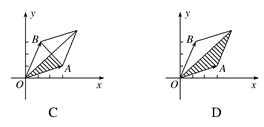
 等于( )
等于( )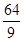
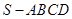 的底面是正方形,
的底面是正方形,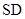 ⊥平面
⊥平面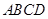 ,
,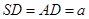 ,点E是SD上的点,且
,点E是SD上的点,且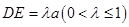 .
.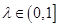 ,都有AC⊥BE;
,都有AC⊥BE;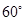 ,求
,求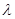 的值
的值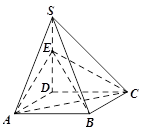
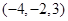 关于坐标平面xoy及y轴的对称点的坐标分别是(a,b,c)、(e,f,d), 则c与e的和为
关于坐标平面xoy及y轴的对称点的坐标分别是(a,b,c)、(e,f,d), 则c与e的和为  ,则该点的坐标
,则该点的坐标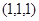
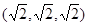
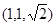
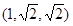
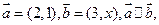 则
则