题目内容
10.数列1,$\frac{1}{2}$,$\frac{2}{2}$,$\frac{1}{3}$,$\frac{2}{3}$,$\frac{3}{3}$,…,$\frac{1}{n}$,$\frac{2}{n}$,…,$\frac{n}{n}$,…的前18项和为11.分析 利用等差数列的前n项和公式即可得出.
解答 解:∵$\frac{1}{n}$+$\frac{2}{n}$+…+$\frac{n}{n}$=$\frac{1+2+…+n}{n}$=$\frac{\frac{n(1+n)}{2}}{n}$=$\frac{1+n}{2}$,
又1+2+3+4+5+3=18,
∴此数列的前18项和=$\frac{1+1}{2}$+$\frac{1+2}{2}$+…+$\frac{1+5}{2}$+$\frac{1+2+3}{6}$
=$\frac{5+\frac{5(1+5)}{2}}{2}$+1
=11.
故答案为:11.
点评 本题考查了等差数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
15.如图,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )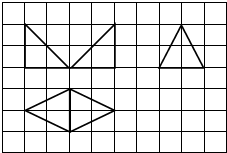

| A. | $\frac{3}{4}$ | B. | $\frac{8}{3}$ | C. | $\frac{16}{3}$ | D. | 8 |