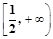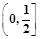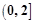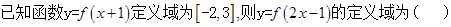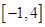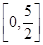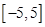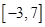题目内容
定义在R上的函数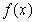 ,对任意的
,对任意的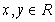 ,有
,有
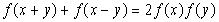 ,且
,且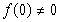 .
.
(1) 求证: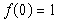 ; (2)求证:
; (2)求证: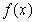 是偶函数.
是偶函数.
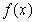 ,对任意的
,对任意的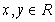 ,有
,有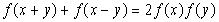 ,且
,且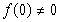 .
.(1) 求证:
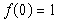 ; (2)求证:
; (2)求证: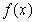 是偶函数.
是偶函数.(1)证明略
(2)证明略
(2)证明略
(1)根据x,y取值的任意性,可令x=y=0可得2f(0)=2f2(0),又因为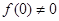 ,从而得
,从而得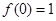 .
.
(2)令x=0可得f(y)+f(-y)=2f(0)f(y)=2f(y),所以f(-y)=f(y),从而可证出f(x)为偶函数
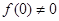 ,从而得
,从而得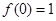 .
.(2)令x=0可得f(y)+f(-y)=2f(0)f(y)=2f(y),所以f(-y)=f(y),从而可证出f(x)为偶函数

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
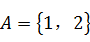 ,
,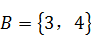 ,请画出从集合
,请画出从集合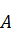 到集合
到集合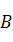 的所有函数关系,并写出每种函数关系中的定义域及值域.
的所有函数关系,并写出每种函数关系中的定义域及值域. 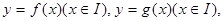 若对于任意
若对于任意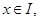 存在
存在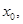 使得
使得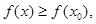
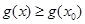 且
且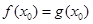 ,则称
,则称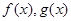 为“兄弟函数”.已知
为“兄弟函数”.已知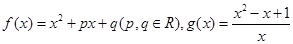 是定义在区间
是定义在区间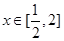 上的“兄弟函数”,那么函数
上的“兄弟函数”,那么函数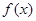 在区间
在区间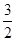
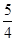
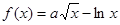
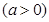
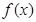 在
在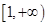 上递增,求
上递增,求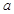 的取值范围;
的取值范围;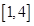 上的最小值.
上的最小值. ,若
,若 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的 ,总有
,总有 ,则实数
,则实数 的取值范围是( )
的取值范围是( )



 ,满足
,满足 ,且当
,且当 时,
时, ,则
,则 的值为( )
的值为( )



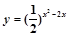 的值域为( )
的值域为( )