题目内容
在平面直角坐标系中,已知定点A(-2,0)、B(2,0),异于A、B两点的动点P满足 ,其中k1、k2分别表示直线AP、BP的斜率.
,其中k1、k2分别表示直线AP、BP的斜率.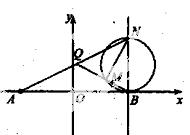
(Ⅰ)求动点P的轨迹E的方程;
(Ⅱ)若N是直线x=2上异于点B的任意一点,直线AN与(I)中轨迹E交予点Q,设直线QB与以NB为直径的圆的一个交点为M(异于点B),点C(1,0),求证:|CM|·|CN| 为定值.
(Ⅰ) ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)根据斜率公式,有斜率乘积等于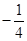 整理即得,注意
整理即得,注意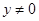 ;(Ⅱ)设直线
;(Ⅱ)设直线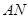 的方程,与椭圆方程组成方程组,消去
的方程,与椭圆方程组成方程组,消去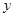 ,由韦达定理求点
,由韦达定理求点 的坐标,根据直线
的坐标,根据直线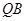 与以
与以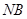 为直径的圆的另一个交点为
为直径的圆的另一个交点为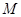 ,得
,得 ,从而得到直线
,从而得到直线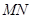 的方程,确定恒过的定点.证明
的方程,确定恒过的定点.证明 三点共线,又
三点共线,又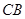 是以
是以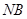 为直径的圆的切线,由切割线定理可知,
为直径的圆的切线,由切割线定理可知,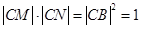 ,即为定值.
,即为定值.
试题解析:(Ⅰ)设 ,由
,由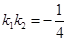 得
得 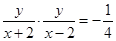 ,其中
,其中 ,
,
整理得 点的轨迹方程为
点的轨迹方程为 . (4分)
. (4分)
(Ⅱ)设点 ,则直线
,则直线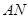 的方程为
的方程为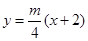 ,
,
解方程组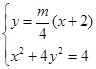 ,消去
,消去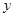 得
得 ,
,
设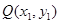 ,则
,则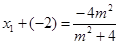 ,
,
 ,
,
从而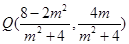 ,又
,又 ,
,
 直线
直线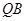 与以
与以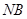 为直径的圆的另一个交点为
为直径的圆的另一个交点为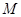 ,
,
 ,
,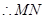 方程为
方程为 ,即
,即 ,过定点
,过定点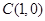 , (9分)
, (9分)
定值证法一:即 三点共线,又
三点共线,又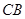 是以
是以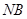 为直径的圆的切线,由切割线定理可知,
为直径的圆的切线,由切割线定理可知,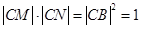 ,为定值. (12分)
,为定值. (12分)
定值证法二:直线 :
: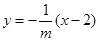 ,直线
,直线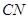 :
: ,
,
联立得,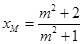 ,
,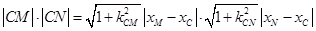
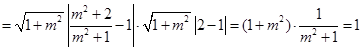 ,为定值. (12分)
,为定值. (12分)
考点:椭圆方程,直线与椭圆的关系,定点、定值问题.

练习册系列答案
 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
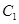 的参数方程为
的参数方程为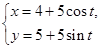 (
(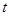 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线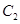 的极坐标方程为
的极坐标方程为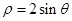 .
.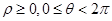 ).
). 中,已知点
中,已知点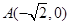 ,
,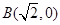 ,
,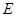 为动点,且直线
为动点,且直线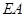 与直线
与直线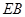 的斜率之积为
的斜率之积为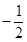 .
.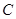 的方程;
的方程;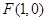 的直线
的直线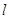 与曲线
与曲线 ,
, .若点
.若点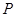 在
在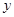 轴上,且
轴上,且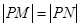 ,求点
,求点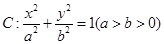 的离心率为
的离心率为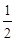 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线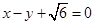 相切,直线
相切,直线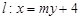 与椭圆C相交于A、B两点.
与椭圆C相交于A、B两点.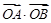 的取值范围;
的取值范围;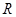 :
: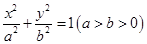 的长轴长为4,且过点
的长轴长为4,且过点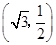 .
. 、
、 、
、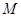 是椭圆上的三点,若
是椭圆上的三点,若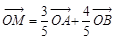 ,点
,点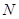 为线段
为线段 的中点,
的中点, 、
、 两点的坐标分别为
两点的坐标分别为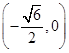 、
、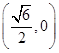 ,求证:
,求证: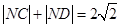 .
. 的左右焦点为F1,F2,离心率为
的左右焦点为F1,F2,离心率为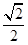 ,以线段F1 F2为直径的圆的面积为
,以线段F1 F2为直径的圆的面积为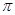 , (1)求椭圆的方程;(2) 设直线l过椭圆的右焦点F2(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.
, (1)求椭圆的方程;(2) 设直线l过椭圆的右焦点F2(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.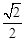 的椭圆C:
的椭圆C: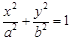 (a>b>0)的左、右焦点,直线
(a>b>0)的左、右焦点,直线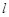 :x=-
:x=-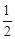 将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.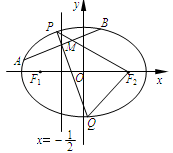
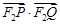 的取值范围.
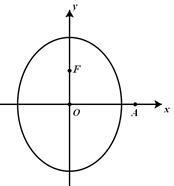
的取值范围. 的对称中心为坐标原点,上焦点为
的对称中心为坐标原点,上焦点为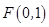 ,离心率
,离心率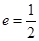 .
.
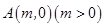 为
为 轴上的动点,过点
轴上的动点,过点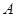 作直线
作直线 与直线
与直线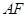 垂直,试探究直线
垂直,试探究直线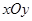 中,已知椭圆
中,已知椭圆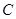 :
: 的离心率
的离心率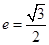 ,且椭圆C上一点
,且椭圆C上一点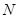 到点Q
到点Q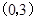 的距离最大值为4,过点
的距离最大值为4,过点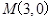 的直线交椭圆
的直线交椭圆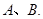
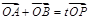 (O为坐标原点),当
(O为坐标原点),当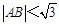 时,求实数
时,求实数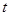 的取值范围.
的取值范围.