题目内容
在平面直角坐标系 中,已知点
中,已知点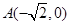 ,
,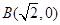 ,
,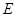 为动点,且直线
为动点,且直线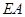 与直线
与直线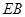 的斜率之积为
的斜率之积为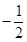 .
.
(1)求动点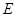 的轨迹
的轨迹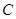 的方程;
的方程;
(2)设过点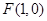 的直线
的直线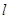 与曲线
与曲线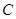 相交于不同的两点
相交于不同的两点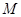 ,
,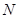 .若点
.若点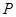 在
在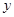 轴上,且
轴上,且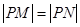 ,求点
,求点 的纵坐标的取值范围.
的纵坐标的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:本题主要考查椭圆的标准方程、直线方程、中点坐标公式等基础知识,突出解析几何的基本思想和方法的考查:如数形结合思想、分类讨论思想、坐标化方法等.第一问,设出动点坐标,利用斜率的关系列出表达式,整理出方程;第二问,先根据直线的斜率是否存在进行讨论,当斜率存在时,设出直线方程,因为相交,所以联立方程,消参,得到关于 的方程,找到
的方程,找到 中点坐标,因为
中点坐标,因为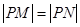 ,所以找直线
,所以找直线 的垂直平分线,令
的垂直平分线,令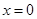 ,得到纵坐标,讨论
,得到纵坐标,讨论 的正负,利用基本不等式得到范围.
的正负,利用基本不等式得到范围.
试题解析:(1)设动点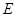 的坐标为
的坐标为 ,依题意可知
,依题意可知 ,
,
整理得 . 3分
. 3分
所以动点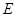 的轨迹
的轨迹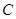 的方程为
的方程为 . 5分
. 5分
(2)当直线 的斜率不存在时,满足条件的点
的斜率不存在时,满足条件的点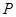 的纵坐标为
的纵坐标为 . 7分
. 7分
当直线 的斜率存在时,设直线
的斜率存在时,设直线 的方程为
的方程为 .
.
将 代入
代入 并整理得,
并整理得, .
.  . 8分
. 8分
设 ,
, ,则
,则 ,.
,.
设 的中点为
的中点为 ,则
,则 ,
, ,
,
所以 . 10分
. 10分
由题意可知 ,
,
又直线 的垂直平分线的方程为
的垂直平分线的方程为 .
.
令 解得
解得 . . 11分
. . 11分
当 时,因为
时,因为 ,所以
,所以 ;
;
当 时,因为
时,因为 ,所以
,所以 . . 13分
. . 13分
综上所述,点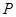 纵坐标的取值范围是
纵坐标的取值范围是 . . 14分
. . 14分
考点:1.椭圆的标准方程;2.中点坐标公式;3.垂直平分线方程;4.基本不等式.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
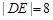 ,动点C的运动轨迹为曲线G,且当动点C运动时,
,动点C的运动轨迹为曲线G,且当动点C运动时,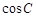 有最小值
有最小值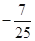 .
.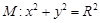 (其中
(其中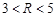 )于A、B两点,求|AB|的取值范围.
)于A、B两点,求|AB|的取值范围. ,0),B(
,0),B(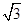 ,0),直线AM、BM相交于点M,且它们的斜率之积为
,0),直线AM、BM相交于点M,且它们的斜率之积为 .
.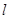 过点F(1,0)且绕F旋转,
过点F(1,0)且绕F旋转, 相交于P、Q两点,
相交于P、Q两点,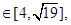 求△
求△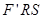 的面积的最大值和最小值(F′为轨迹C的左焦点).
的面积的最大值和最小值(F′为轨迹C的左焦点). 焦点为
焦点为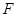 ,直线
,直线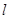 经过点
经过点 相交于
相交于 ,
, 两点
两点 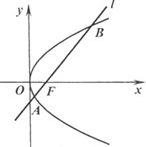
 的中点在直线
的中点在直线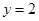 上,求直线
上,求直线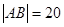 ,求直线
,求直线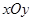 中,点
中,点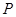 到两点
到两点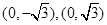 的距离之和等于4,设点
的距离之和等于4,设点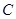 ,直线
,直线 与
与 两点.
两点.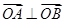 ,求
,求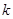 的值.
的值.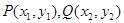 是抛物线
是抛物线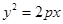
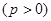 上相异两点,
上相异两点,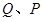 到y轴的距离的积为
到y轴的距离的积为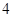 且
且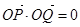 .
.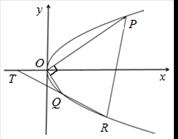
 轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值.
轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值. ,其中k1、k2分别表示直线AP、BP的斜率.
,其中k1、k2分别表示直线AP、BP的斜率.
 与曲线
与曲线 相交于
相交于 、
、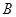 、
、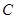 、
、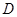 四个点.
四个点. 的取值范围;
的取值范围;  的面积的最大值及此时对角线
的面积的最大值及此时对角线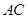 与
与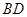 的交点坐标.
的交点坐标.