题目内容

如图所示，过点P(1,2)的直线l交x轴、y轴的正向于A、B两点，求△AOB的面积取最小值时，直线l的方程.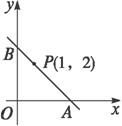

解析：由于所求直线与x轴、y轴各有一个交点，如题图所示，故直线l的斜率一定存在且不等于0.

设直线l的方程为y=kx+b,b＞0.

∵点P(1,2)在直线l上，∴2=k+b,即k=2-b.

令y=0，得xa=-=.由于k＜0,∴2-b＜0,即b＞2.

∴S△AOB=··b===［(b-2)++4］.

则b-2+≥2=4,

当且仅当b-2=2,即b=4时上述不等式取等号，此时k=2-b=-2.

故所求直线的方程为y=-2x+4,即2x+y-4=0.

练习册系列答案
相关题目
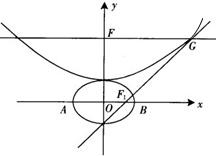精英家教网设b＞0，椭圆方程为
x2
2b2
+
y2
b2
=1，抛物线方程为y=
1
8
x2+b，如图所示，过点F（0，b+2）作x轴的平行线，与抛物线在第一象限的交点为G，已知抛物线在点G处的切线经过椭圆的右焦点F1．
（1）求点G和点F1的坐标（用b表示）；
（2）求满足条件的椭圆方程和抛物线方程；
（3）设A，B分别是椭圆长轴的左、右端点，试探究在抛物线上是否存在点P，使得△ABP为直角三角形？若存在，指出共有几个这样的点？并说明理由（不必具体求出这些点的坐标）．
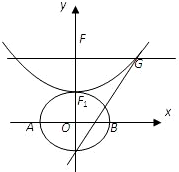精英家教网设b＞0，椭圆方程为
x2
2b2
+
y2
b2
=1，抛物线方程为x2=8（y-b）．如图所示，过点F（0，b+2）作x轴的平行线，与抛物线在第一象限的交点为G，已知抛物线在点G的切线经过椭圆的右焦点F1．
（1）求满足条件的椭圆方程和抛物线方程；
（2）设A，B分别是椭圆长轴的左、右端点，试探究在抛物线上是否存在点P，使得△ABP为直角三角形？若存在，请指出共有几个这样的点？并说明理由（不必具体求出这些点的坐标）．
如图所示，过点M（-6，0）作圆C：x2+y2-6x-4y+9=0的割线，交圆C于A、B两点．
（1）求线段AB的中点P的轨迹；
（2）在线段AB上取一点Q，使
1
MA
+
1
MB
=
2
MQ
，求点Q的轨迹．

如图所示，过点P(－1，2)的直线l与线段AB相交，若A(－2，－3)，B(3，0)，求直线l斜率的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网