题目内容
 设b>0,椭圆方程为
设b>0,椭圆方程为| x2 |
| 2b2 |
| y2 |
| b2 |
| 1 |
| 8 |
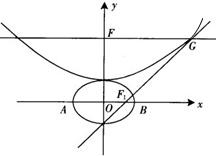
(1)求点G和点F1的坐标(用b表示);
(2)求满足条件的椭圆方程和抛物线方程;
(3)设A,B分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点P,使得△ABP为直角三角形?若存在,指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
分析:(1)直接可以写出;
(2)利用抛物线在点G处的切线经过椭圆的右焦点F1可以求得;
(3)将直角关系转化为数量积为0,从而求出满足条件的三角形的个数.
(2)利用抛物线在点G处的切线经过椭圆的右焦点F1可以求得;
(3)将直角关系转化为数量积为0,从而求出满足条件的三角形的个数.
解答:解:(1)G点的坐标为(4,b+2)…(2分)
由椭圆方程得F1点的坐标为(2-b,0)
(2)由y=
x2+b得,y′=
x,y'|x=4=1,…(2分)
过点G的切线方程为y-(b+2)=x-4即y=x+b-2…(2分)F1点的坐标(b,0)代入得b=1
即椭圆和抛物线的方程分别为
+y2=1和y=
x2+1;…(2分)
(3)∵过A作x轴的垂线与抛物线只有一个交点P,∴以∠PAB为直角的Rt△ABP只有一个,
同理:以∠PBA为直角的Rt△ABP只有一个.…(2分)
若以∠APB为直角,设P点坐标为(x,
x2+1),A、B两点的坐标分别为(-
,0)和(
,0),
•
=x2-2+(
x2+1)2=
x4+
x2-1=0.
关于x2的二次方程有一大于零的解,∴x有两解,
即以∠APB为直角的Rt△ABP有两个,…(2分)
因此抛物线上存在四个点使得△ABP为直角三角形.…(1分)
由椭圆方程得F1点的坐标为(2-b,0)
(2)由y=
| 1 |
| 8 |
| 1 |
| 4 |
过点G的切线方程为y-(b+2)=x-4即y=x+b-2…(2分)F1点的坐标(b,0)代入得b=1
即椭圆和抛物线的方程分别为
| x2 |
| 2 |
| 1 |
| 8 |
(3)∵过A作x轴的垂线与抛物线只有一个交点P,∴以∠PAB为直角的Rt△ABP只有一个,
同理:以∠PBA为直角的Rt△ABP只有一个.…(2分)
若以∠APB为直角,设P点坐标为(x,
| 1 |
| 8 |
| 2 |
| 2 |
| PA |
| PB |
| 1 |
| 8 |
| 1 |
| 64 |
| 5 |
| 4 |
关于x2的二次方程有一大于零的解,∴x有两解,
即以∠APB为直角的Rt△ABP有两个,…(2分)
因此抛物线上存在四个点使得△ABP为直角三角形.…(1分)
点评:本题综合性强,解题时应注意充分利用条件,将解析几何与导数、向量巧妙地结合起来

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 设b>0,椭圆方程为
设b>0,椭圆方程为 (本小题满分14分)设b>0,椭圆方程为
(本小题满分14分)设b>0,椭圆方程为 (本小题满分14分)设b>0,椭圆方程为
(本小题满分14分)设b>0,椭圆方程为 设b>0,椭圆方程为
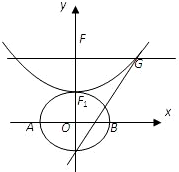
设b>0,椭圆方程为 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.