题目内容
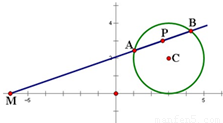
 如图所示,过点M(-6,0)作圆C:x2+y2-6x-4y+9=0的割线,交圆C于A、B两点.
如图所示,过点M(-6,0)作圆C:x2+y2-6x-4y+9=0的割线,交圆C于A、B两点.(1)求线段AB的中点P的轨迹;
(2)在线段AB上取一点Q,使
| 1 |
| MA |
| 1 |
| MB |
| 2 |
| MQ |
分析:(1)设中点P的坐标,建立关于点P的方程,从而确定轨迹方程.
(2)利用代入法求点点Q的轨迹.
(2)利用代入法求点点Q的轨迹.
解答:解:(1)圆C的方程为(x-3)2+(y-2)2=4,其圆心为C(3,2),半径为2.
又M∈{M|PC⊥MP,P在已知圆内},
设P点坐标(x,y),则CP的斜率为
(x≠3),MP的斜率为
(x≠-6),
所以
•
=-1,化简得x2+y2+3x-2y-18=0.
点C(3,2)应在轨迹上,而x=3时,y=2满足方程x2+y2+3x-2y-18=0,
所以点P的轨迹是圆x2+y2+3x-2y-18=0在已知圆内的一段弧.
(2)设A(x1,y1),B(x2,y2),Q(x,y),直线AB的斜率为k,则有MA=
(x1+6), MB=
(x2+6),MQ=
(x+6),
代入
+
=
,有
+
=
,
即
=
,①
把y=k(x+6)代入x2+y2-6x-4y+9=0,得(k2+1)x2+2(6k2-2k-3)x+3(12k2-8k+3)=0,x1+x2=-
,x1•x2=
,②
②代入①并化简得
=
⇒2k(x+6)+9x-27=0,而k=
,从而有9x+2y-27=0,所以点Q的轨迹是直线9x+2y-27=0的圆内部分.
又M∈{M|PC⊥MP,P在已知圆内},
设P点坐标(x,y),则CP的斜率为
| y-2 |
| x-3 |
| y |
| x+6 |
所以
| y-2 |
| x-3 |
| y |
| x+6 |
点C(3,2)应在轨迹上,而x=3时,y=2满足方程x2+y2+3x-2y-18=0,
所以点P的轨迹是圆x2+y2+3x-2y-18=0在已知圆内的一段弧.
(2)设A(x1,y1),B(x2,y2),Q(x,y),直线AB的斜率为k,则有MA=
| 1+k2 |
| 1+k2 |
| 1+k2 |
代入
| 1 |
| MA |
| 1 |
| MB |
| 2 |
| MQ |
| 1 |
| x1+6 |
| 1 |
| x2+6 |
| 2 |
| x+6 |
即
| 2 |
| x+6 |
| x1+x2+12 |
| x1x2+6(x1+x2)+36 |
把y=k(x+6)代入x2+y2-6x-4y+9=0,得(k2+1)x2+2(6k2-2k-3)x+3(12k2-8k+3)=0,x1+x2=-
| 2(6k2-2k-3) |
| k2+1 |
| 3(12k2-8k+3) |
| k2+1 |
②代入①并化简得
| 2 |
| x+6 |
| 4k+18 |
| 81 |
| y |
| x+6 |
点评:本题考查直线与圆的位置关系,考查轨迹方程,运算量较大,综合性较强.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图所示,过点P (0,-2)的直线l交抛物线y2=4x于A,B两点,求以OA,OB为邻边的平行四边形OAMB的顶点M的轨迹方程.
如图所示,过点P (0,-2)的直线l交抛物线y2=4x于A,B两点,求以OA,OB为邻边的平行四边形OAMB的顶点M的轨迹方程. (本小题满分14分)设b>0,椭圆方程为
(本小题满分14分)设b>0,椭圆方程为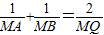 ,求点Q的轨迹.
,求点Q的轨迹.