题目内容
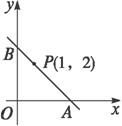
如图所示,过点P(-1,2)的直线l与线段AB相交,若A(-2,-3),B(3,0),求直线l斜率的取值范围.

答案:
解析:
解析:
|
探究过程:方法一:kPA= 因为过点P的直线PC的斜率不存在, 而[0, 所以直线l的斜率的取值范围是(-∞,- 方法二:设直线l的斜率为k(斜率存在时),则直线l的方程为y-2=k(x+1),即kx-y+k+2=0.因为直线l与线段AB相交,所以A,B两点在直线l的两侧或其中一点在直线上,所以将A,B的坐标代入kx-y+k+2所得结果异号或等于0,即(-2k+3+k+2)(3k+k+2)≤0,解得k≤- 探究结论:有些问题并看不出是二元一次不等式(组)问题,经过多方位、多角度的思考和信息迁移等,可以转化为二元一次不等式(组)问题求解.本题第一种方法是常规法,采用了数形结合思想以及正切函数的单调性求解,方法二比较巧妙,通过观察和思考,发现可以转化为二元一次不等式表示平面区域的方法解题,并且逆用了这一知识点,显得思路更为开阔、清晰. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,过点P (0,-2)的直线l交抛物线y2=4x于A,B两点,求以OA,OB为邻边的平行四边形OAMB的顶点M的轨迹方程.
如图所示,过点P (0,-2)的直线l交抛物线y2=4x于A,B两点,求以OA,OB为邻边的平行四边形OAMB的顶点M的轨迹方程.